2.会依据不等式的性质对不等式进行变形．

1.理解并掌握不等式的二个性质．

6.小结：

5.思考：

①不等式的两边都乘以0，会出现什么样的结果？

②不等式的性质与等式的性质有什么相同点、不同点？

4.练习：课本P₁₄练习1-3

3.操作：将不等式5﹥3的两边分别乘以同一个数，用不等号填空：

5×1(　 )3×1，

5×2(　 )3×2，

5×3(　 )3×3，

5×4(　 )3×4，

…

5×(-1)(　 )3×(-1)，

5×(-2)(　 )3×(-2)，

5×(-3)(　 )3×(-3)，

5×(-4)(　 )3×(-4)，

…

在小组中讨论，你发现了什么？

概括：

不等式性质2：如果a＞b，并且c＞0，那么ac＞bc．?

不等式性质3：如果a＞b，并且c＜0，那么ac＜bc．?

用语言表述为：

不等式的两边都乘以(或除以)同一个正数，不等号的方向不变．

不等式的两边都乘以(或除以)同一个负数，不等号的方向改变．

2.试验：

① 有甲、乙两同学，甲的钱多于乙的钱，然后再给甲、乙两人相同的钱，则甲、乙两人的钱谁多谁少？如果都捐出同样的钱，情况又会如何？ (甲的钱肯定还是多于乙的钱)

② 如图所示：

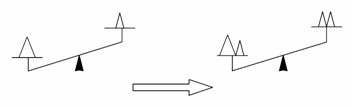
　?　　　　　 a＞b??　　　　　　　 a+c＞b+c?

从左侧看：从天平中可以看出　 a＞b．?

从右侧看：天平两边加上等量的砝码c，天平的状态还像原来那样．

概括

不等式性质1：如果a＞b，那么a+c＞b+c，a－c＞b－c．?

用语言表述为：

不等式两边都加上(或减去)同一个数或同一个整式，不等号方向不变．

1.引入

解一元一次方程时，我们主要对方程进行如下变形：

①去分母；②移项；③合并同类项；④化未知数的系数为1．

在研究不等式时，我们同样要探究不等式的变形规律．

2. 等式的基本性质是什么？

　[活动设计]

1. 解方程 3x－4＝5x－5．?

解：3x－5x＝－5+4?　 ……移项

?　　 －2x＝－1?……合并同类项

?　　　 x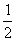＝?……系数化1