
2. 爸爸的年龄a比儿子的年龄b大,再过10年,爸爸的年龄仍比儿子年龄大,即:a>b a+10>b+10。
爸爸的年龄a比儿子的年龄b大,再过10年,爸爸的年龄仍比儿子年龄大,即:a>b a+10>b+10。
1.等式的基本性质是什么?
(1) 等式的两边同时加上(或减去)同一个数或同一个整式,相等关系仍然成立。
(2) 等式的两边同时乘以(或除以)不为零的同一个数或同一个整式,相等关系仍然成立。
3.思考题:
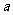 是任意有理数,试比较5
是任意有理数,试比较5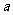 与3
与3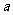 的大小。
的大小。
课堂作业
课本P14习题7.3-1、2
[设计说明]
本课内容重点是推导不等式的性质,为不等式的变形作准备,在推导不等式的性质的过程中,发展学生的观察、比较、归纳的能力,渗透类比的数学思想。在活动设计上,着力通过观察、比较、操作、类比、思考等环节,着重让学生参与到这个过程中来,体现了主体性的原则。本课教材没有安排例题,考虑到学生的基础较差,补充了变形的例题。
2.比较下列各题两式的大小:
(1)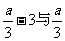 ; (2)
; (2)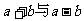 ; (3)
; (3)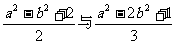
1.根据不等式的性质,把下列不等式化为x>a或x<a的形式(a为常数):
(1)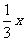 >
> ;
(2)
;
(2) ;
;
(3) >2;
(4)
>2;
(4)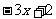 <
<
4.(1)用“>”号或“<”号填空,并简说理由。
① 6+2 -3+2; ② 6×(-2) -3×(-2);
③ 6÷2 -3÷2; ④ 6÷(-2) -3÷(-2)
(2)如果a>b,则
① 
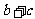 ②
② 

③ 
 >0)
④
>0)
④ 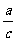
 (c<0)
(c<0)
课后作业
3. 利用不等式的基本性质,填“>”或“<”:
(1)若a>b,则2a+1 2b+1;
(2)若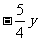 <10,则y
-8;
<10,则y
-8;
(3)若a<b,且c>0,则ac+c bc+c;
(4)若a>0,b<0, c<0,(a-b)c 0。
2.将下列不等式改写成“x>a”或“x<a”的形式:
(1) >0; (2)
>0; (2) <4。
<4。
1.已知x<y,用“<”或“>”号填空。
(1) ; (2)
; (2)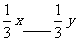 ; (3)
; (3) ; (4)
; (4) ;
;
3.要注意应用不等式性质2时(负数)不等号的变化问题.
[例题设计]
补充例题:将下列不等式化成“x>a”或“x<a”的形式:
(1)x-5>-1;
(2)-2x>3;
(3)3x<-9.
[生](1)根据不等式的基本性质1,两边都加上5,得
x>-1+5
即x>4;
(2)根据不等式的基本性质3,两边都除以-2,得
x<- ;
;
(3)根据不等式的基本性质2,两边都除以3,得
x<-3.
说明:在不等式两边同时乘以或除以同一个数(除数不为0)时,要注意数的正、负,从而决定不等号方向的改变与否.
[练习设计]
课内作业
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com