
4.解下列不等式:
(1)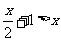 ;
(2)
;
(2)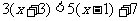 ;
;
(3)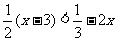 ;
;
3. a取什么值时,代数式4a+2的值
(1)大于1? (2)等于1? (3)小于1?
2.解下列不等式,并把解集在数轴上表示出来:
(1)2x+1>3; (2)2-x<1;
(3)2(x+1)<3x; (4)3(2x+2)≥4(x-1)+7.
1.下面方程或不等式的解法对不对?为什么?
(1)
由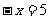 , 得
, 得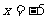 ;
;
(2)
由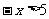 ,得
,得 ;
;
(3)
由 ,得
,得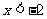 ;
;
(4)
由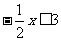 ,得
,得 .
.
解下列不等式并把它的解集在数轴上表示出来:
(1)x-8<3; (2)3x>7;
(3)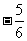 x-1≤2. (要求学生能够说出变形的方法和其依据)
x-1≤2. (要求学生能够说出变形的方法和其依据)
问: 通过以上例题的解答,我们来总结一下一元一次不等式的解法,并和一元一次方程的解法作一下比较,看看他们有哪些类似之处?有什么不同?(可安排学生进行讨论和交流.)
由学生得出以下结论,教师作适当的总结.
(1)解一元一次不等式的一般步骤: 去分母,去括号,移项,合并同类项,系数化为1.
(2)解一元一次不等式和解一元一次方程步骤类似,但要注意在不等式两边都乘以(或除以)同一个负数时,不等号方向必须改变.
小华在3月初栽种了一棵小树,小树高75cm,小树成活后每周长高2.5cm,估计几周后这棵小树超过100cm.
解:设x周后这棵小树的高度超过100cm.
根据题意,得
这个不等式的解集在数轴上表示如下:

问: 这些不等式中含有几个未知数,未知数的次数是多少,含有未知数的式子是什么样的代数式?这些不等式有一个共同的特点:
只含有一个未知数,并且未知数的最高次数是1,系数不等于0,这样的不等式叫做一元一次不等式(linear inequality with one unknown).
说明:它们都只含有一个未知数,且含未知数的式子是整式,未知数的次数是1.
2.解下列不等式,并把解集在数轴上表示出来.
(1) 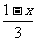 <-1; (2)6-(x-1)<1.
<-1; (2)6-(x-1)<1.
1.直接写出下列一元一次不等式的解集.
(1)-x<2; (2)1-x <x-1;
(3)2x-3>1; (4)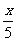 ≤x.
≤x.
(四)总结、扩展
这节课我们学习了积的乘方的运算性质,请同学们谈一下你对本节课学习的体会.
学生活动:谈这节课的主要内容或注意问题等等.
[教法说明]课堂归纳总结由学生来说,可以使学生上课听讲精神集中,还可以训练学生归纳总结的能力.
(三)教学过程
1.创设情境,复习导入
前面我们学习了同底数幂的乘法、幂的乘方这两个寨的运算性质,请同学们通过完成一组练习,来回顾一下这两个性质:
填空:
(1)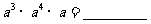 (2)
(2)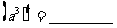
(3)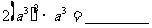 (4)
(4)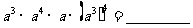
学生活动:4个学生说出答案,同桌同学给予判断.
[教法说明]通过完成本练习,进一步巩固、理解同底数幂的乘法,幂的乘方,同时也为顺利完成本节例2做个铺垫.
2.探索新知,讲授新课
我们知道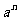 表示
表示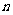 个
个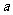 相乘,那么
相乘,那么
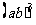 表示什么呢?(注意:
表示什么呢?(注意: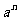 中
中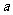 具有广泛性)
具有广泛性)
学生回答时,教师板书.
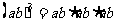
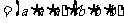 这又根据什么呢?(学生回答乘法交换律、结合律)
这又根据什么呢?(学生回答乘法交换律、结合律)
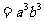
也就是 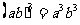
请同学们回答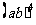 、
、 、
、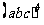 、
、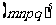 的结果怎样?那么
的结果怎样?那么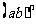 (
(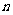 是正整数)如何计算呢?
是正整数)如何计算呢?
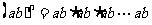 ;____________个
;____________个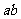
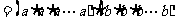 运用了________律和________律
运用了________律和________律
________个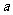 ________个
________个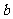

学生活动:学生完成填空.
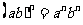 (
(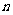 是正整数)
是正整数)
刚才我们计算的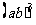 、
、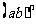 是什么运算?(答:乘方运算)什么的乘方?(积的乘方)
是什么运算?(答:乘方运算)什么的乘方?(积的乘方)
通过刚才的推导,我们已经得到了积的乘方的运算性质.
请同学们用文字叙述的形式把它概括出来.
学生活动:学生总结,并要求同桌相互交流,互相纠正补充.达成一致后,举手回答,其他学生思考,准备更正或补充.
[教法说明]通过学生自己概括总结,既培养了学生的参与意识,又训练了他们归纳及口头表达能力.
教师根据学生的概括给予肯定或否定,纠正后板书.
积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
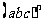 运算形式
运算方法
运算结果
运算形式
运算方法
运算结果
提出问题:这个性质对于三个或三个以上因式的积的乘方适用吗?如
学生活动:在运算的基础上给出答案.
|
3.尝试反馈,巩固知识
例1 计算:
(1)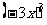 (2)
(2)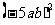
(3) (4)
(4)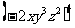
学生活动:每一题目均由学生说出完整的解题过程.
解:(1)原式
(2)原式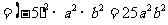
(3)原式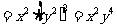
(4)原式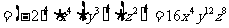
[教法说明]对例1的处理,要充分调动学生的参与意识,训练学生运用已有知识去解决新问题的能力,同时,在学生“说”,教师“写”的过程中,教师可随时发现并及时纠正学生解题中出现的问题,如(1)(2)(4)小题中“-”号的处理,并强调解题程序以及幂的乘方性质的运用,同时提出把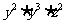 着做一个数进行运算.
着做一个数进行运算.
练习一
(1)计算:(回答)
①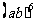 ②
②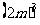 ③
③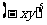 ④
④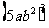
(2)计算:
①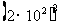 ②
②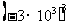
③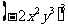 ④
④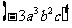
(3)下面的计算对不对?如果不对,应怎样改正?
①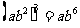 ②
②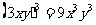 ③
③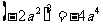
学生活动:第(1)题由4个学生口答,同桌或其他学生给予判断.
第(2)题在练习本上完成,同桌或前后桌互阅,教师抽查.
第(3)题由学生回答.
[教法说明]通过第(1)题可检查学生对性质掌握的熟练程度.第(2)题学生互阅主要是让学生相互交流,培养学生的参与意识.若出现问题由同学指出,有时比老师指出效果要好.第(3)题中的错误是学生应用性质时易出现的,所以在学生回答时,教师对每个问题都应予以强调.
4.综合尝试,巩固知识
例2 计算:
(1)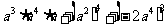
(2)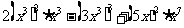
学生活动:学生分成两组,每组各做一题,各派一个学生板演.
[教法说明]
学生已具备综合运用性质的能力,让学生尝试解题,目的是训练学生分析问题的能力.分组练习,不仅能激发学生的兴趣,同时也可培养学生的集体荣誉感.学生对知识的印象会更深刻.
5.反复练习,加深印象
练习二
计算:
(1)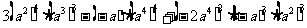
(2)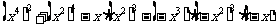
学生活动:学生在练习本上完成,找两个学生板演.
[教法说明]此时学生已能准确运用幂的三种运算性质进行计算,但在计算过程中还会出现各种问题,所以在学生板演时,师生共同订正,可减少不必要的错误出现.
6.变式训练,培养能力
练习三
填空:
(1) (2)
(2)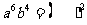
(3)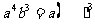 (4)
(4)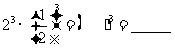
(5)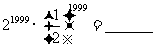
学生活动:四人一组研究,讨论得出结果,然后由小组代表说出答案.
[教法说明]此组题主要是训练学生的逆向思维和发散思维,提高学生的应变能力.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com