
师生共同回顾:
用一元一次不等式解决简单的实际问题时,先要设出未知数,再根据题中不等量关系列出不等式,最后解一元一次不等式
例3 张玲有1元和5角的硬币共15枚,这些硬币的总数大于10.5元.
问张玲至少有多少枚1元的硬币?
分析:以“硬币的总数大于10.5元”为不等量关系,列不等式.
(1)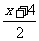 +
+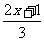 ≥0 (2)
≥0 (2)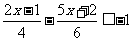
解:去分母,得
去括号,得
移项,合并同类项,得
例2 当x取何值时,代数式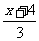 与
与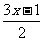 的值的差大于4?
的值的差大于4?
讨论:若将例2改为“代数式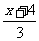 与
与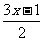 的值的差大于4时,求x 的最大整数解?”
的值的差大于4时,求x 的最大整数解?”
问:把求一元一次不等式的整数解与求一元一次不等式的解集作一下比较,看看他们有哪些类似之处?有什么不同?(可安排学生进行讨论和交流.)
由学生得出以下结论,教师作适当的总结.
(1)解法步骤类似: 去分母,去括号,移项,合并同类项,系数化为1.
(2)求一元一次不等式的整数解比求一元一次方程的解集多一个步骤:就是在解集中找出整数解.
3.(1)解一元一次不等式的一般步骤: 去分母,去括号, ,合并同类项,系数化为1.
(2)解一元一次不等式和解一元一次方程步骤类似,但要注意在不等式两边都乘以(或除以)同一个负数时,不等号方向必须 .
2. 只含有 未知数,并且未知数的最高次数是 ,系数 0,这样的不等式叫做一元一次不等式(linear inequality with one unknown).
1.解下列不等式,并把解集在数轴上表示出来.
(1)14-4x>0; (2)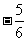 x-1≤2.
x-1≤2.
㈠ 要使下列各式有意义,求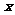 的取值范围:
的取值范围:
① 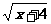 ②
② 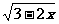 ③
③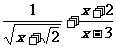 ④
④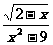
解题思路:二次根号有意义,被开方数应________
 一元一次不等式
一元一次不等式
分式有意义,分母___________
㈡ 填空
适合不等式 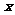 >
>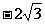 的负整数解是________________
的负整数解是________________
适合不等式 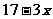 ≥
≥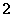 的正整数解是________________
的正整数解是________________
适合不等式 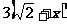 >
>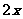 的最小负整数解是________________
的最小负整数解是________________
适合不等式 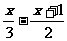 >
>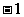 的非负整数解是 ________________
的非负整数解是 ________________
㈢ (1)当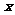 为何值时,
为何值时,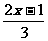 与
与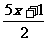 的差不大于
的差不大于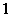 ?
?
(2)求出不等式 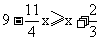 的正整数解。
的正整数解。
⑴ 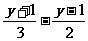 >
>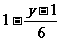 去分母 得
去分母 得
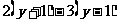 >
>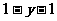
⑵ 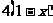 >
>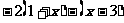 去括号 得
去括号 得
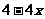 >
>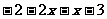
⑶ 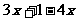 ≤
≤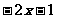 移项 得
移项 得
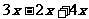 ≤
≤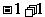
⑷ 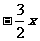 ≥
≥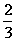 两边同除以
两边同除以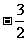 得
得 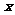 ≥
≥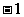
①_____________②______________ ③______________ ④______________⑤________________
练习:解下列不等式
⑴ 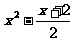 <
<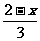 ⑵
⑵ 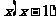 ≥
≥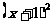
①解一元一次不等式的步骤中的去分母和未知数的系数化1这两步,若乘数或除数是负数,要改变不等号的方向;②一元一次不等式的解集中含有无限多个数;③在解题过程中,要避免解方程中易出现的错误在解不等式中重犯;④对于一元一次不等式的解法步骤,在解题时,要做到灵活运用.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com