
2.解下列不等式,并把解集在数轴上表示出来:
(1)2x+1>3; (2)2-x<1;
(3)2(x+1)<3x; (4)3(2x+2)≥4(x-1)+7.
1.下面方程或不等式的解法对不对?为什么?
(1)
由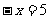 , 得
, 得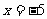 ;
;
(2)
由 ,得
,得 ;
;
(3)
由 ,得
,得 ;
;
(4)
由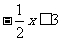 ,得
,得 .
.
解下列不等式并把它的解集在数轴上表示出来:(1)x-8<3; (2)3x>7;
(3)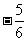 x-1≤2. (要求学生能够说出变形的方法和其依据)
x-1≤2. (要求学生能够说出变形的方法和其依据)
问: 通过以上例题的解答,我们来总结一下一元一次不等式的解法,并和一元一次方程的解法作一下比较,看看他们有哪些类似之处?有什么不同?(可安排学生进行讨论和交流.)
由学生得出以下结论,教师作适当的总结.
(1)解一元一次不等式的一般步骤: 去分母,去括号,移项,合并同类项,系数化为1.
(2)解一元一次不等式和解一元一次方程步骤类似,但要注意在不等式两边都乘以(或除以)同一个负数时,不等号方向必须改变.
练习:课本P.16-练习1、2
辨析练习:
师 我们再来解一些一元一次不等式,并将解集在数轴上表示出来:
(1)2x-1> 4x+13;
解 (1) 2x-1> 4x+13,
2x-4x>13+1, (移项)
-2x>14, (合并同类项)
x>-7. (系数化为1)
它解集在数轴上的表示如图:

观察上述解答有没有错误,为什么?
练习:课本P.18-习题-1、2(1)(2)
小华在3月初栽种了一棵小树,小树高75cm,小树成活后每周长高2.5cm,估计几周后这棵小树超过100cm.
解:设x周后这棵小树的高度超过100cm.
根据题意,得
这个不等式的解集在数轴上表示如下:

问: 这些不等式中含有几个未知数,未知数的次数是多少,含有未知数的式子是什么样的代数式?这些不等式有一个共同的特点:
只含有一个未知数,并且未知数的最高次数是1,系数不等于0,这样的不等式叫做一元一次不等式(linear inequality with one unknown).
说明:它们都只含有一个未知数,且含未知数的式子是整式,未知数的次数是1.
2.解下列不等式,并把解集在数轴上表示出来.
(1) 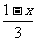 <-1; (2)6-(x-1)<1.
<-1; (2)6-(x-1)<1.
1.直接写出下列一元一次不等式的解集.
(1)-x<2; (2)1-x <x-1;
(3)2x-3>1; (4)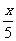 ≤x.
≤x.
4.某校举行庆祝“十六大”的文娱汇演,评出一等奖5个,二等奖10个,三等奖25个,学校决定给获奖的学生发奖品,同一等次的奖品相同,并且只能从下表所列物品中选取一件:
|
品名 |
小提琴 |
运动服 |
笛子 |
舞鞋 |
口琴 |
相册 |
笔记本 |
钢琴 |
|
单价/元 |
120 |
80 |
24 |
22 |
16 |
6 |
5 |
4 |
(1) 如果获奖等次越高,奖品单价就越高,那么学校最少要花多少钱买奖品?
(2) 学校要求一等奖奖品单价是二等奖奖品单价的5倍,二等奖奖品单价是三等奖奖品单价的4倍,在总费用不超过1000元的前提下,有几种购买方案?花费最多的一种方案需多少钱?
课堂作业
课本P18习题7.4-1⑷、⑹
[设计说明]
本课是解不等式第1课时,重点是在类比解方程的基础上得出解不等式的一般步骤,能够较熟练地解简单的一元一次不等式,因此在情境活动与作业的设计上都紧紧围绕这个中心与重心课后作业是供那些学有余力的学生提高所用。对教材提供的情境和探索一元一次不等式的解法作了调整,但在练习中还是特出了教材编写的特点,即生活化、应用化(补充例2、课内作业3等)。
3.甲、乙两家体育用品商店出售同样的乒乓球拍和乒乓球,乒乓球拍每副定价20元,乒乓球定价每盒5元,现两家商店搞促销活动,甲店:每买一副乒乓球拍赠送一盒乒乓球;乙店:按定价的九折优惠。某边需购球拍4副,乒乓球若干盒(不少于4盒)。
(1) 设购买乒乓球盒数为x(盒),在甲商店付款为y甲(元),在乙商店付款为y乙(元),分别写出y甲,y乙与x的关系式;
(2) 就乒乓球盒数讨论去哪家商店买合算?
2.已知方程3(x-2a)+2=x-a+1的解适合不等式2(x-5)≥8a,求a的取值范围。
1.如果关于x的不等式-k-x+6>0的正整数解为1,2,3,正整数k应取怎样的值?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com