2．已知ac²＞bc²，能否推出a＞b?

1．已知a＞b，能否推出ac²＞bc²?

1．课本第14页练习第1、2、3题。

设计说明：培养学生应用不等式性质解不等式能力，进一步熟悉不等式的多个基本性质。　　　

　　 例1根据不等式的性质，将不等式变形成x＞a或x＜a的形式。

　　 (1)x－3＞2；

　　 (2)3x＜2x－3。

　　 例2根据不等式的性质，将不等式变形成x＞a或x＜a的形式。

(1)x＞－3；　　

(2)－2x＜3x+5

3．不等式的两边都乘以(或除以)同一个不为零的数，不等号的方向是否也不变呢?

　　 探索观察：将不等式5＞3的两边都乘以同一个不为0的数，比较所得结果。

　　 用“＜”或“＞”填空：

5×3　 3×3，5×4　 3×4，5×(－2)　 3×(－2)，5×(－0.5)　 3×(－0.5)

5÷3　 3÷3,5÷4　 2÷4，5÷(－2)　 3÷(－2)，5÷(－0.5)　 3÷(－0.5)，

　　 提问：你能从中发现什么?

　 　设计说明：启发学生由特殊过渡到一般，逐步发现规律和通过类比得出规律，得到不等式性质二。

　　 不等式的性质2　 不等式两边都乘以(或除以)同一个正数，不等号的方向不变；不等式两边都乘以(或除以)同一个负数，不等号的方向改变。

　　 用不等式表示为：如果a＞b，并且c＞0，那么ac＞bc；如果a＞b，并且c＜0，那么ac＜bc。

4思考：a：不等式两边都乘0，结果又怎样呢？

b：不等式的性质和等式的性质相比较有什么相同点与不同点？

2．你能否用生活中的例子来说明不等式的性质1呢？　　

1．不等式的性质1　 不等式的两边都加上(或减去)同一个数或同一个整式，不等号的方向不变。

　　 用不等式表示为：如果a＞b，那么a+c＞b+c，a－c＞b－c

　 　说明：由学生通过实际问题，研究、讨论其中所蕴含的数学思想、方法、规律，渗透概括、归纳的方法。

电梯里面有师生两人，老师的身高a米比学生的身高b米要高，当电梯的高度升高6米，老师相对与原来的高度仍比学生高，即：由a＞b 可得　 a+6＞b+6 。当电梯的高度降低6米，老师相对与原来的高度还比学生高，即：由a＞b 可得　 a-6＞b-6 。

设计说明：通过学生所熟悉的事例引导学生猜想并发现不等式性质一。

4．解下列不等式：

　 (1)；　　　　 　　(2)；

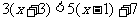　 (3)；　 　

3． a取什么值时，代数式4a+2的值

(1)大于1？ (2)等于1？　 (3)小于1？