
2.判定:一般三角形SAS,ASA,AAS,SSS.
直角三角形,除上述判定外,还有其特殊判定HL.
1.性质:对应边、对应角相等.
基本性质包括各部分名称及基本边角关系,即,1.两边之和大于第三边,两边之差小于第三边;2.三内角和为180°,外角等于不相邻两内角和.外角大于任一不相邻内角.直角三角形两锐角互余.
分类包括按边分为
按角分为
7.4 认识三角形(二)
|
课 题 |
7.4 认识三角形(二) |
课 型 |
新 授 课 |
||||
|
教 学 目 标 |
知识目标 |
通过学生动手操作,理解三角形的角平分线、中线和高等几个概念,并会正确画出任意一个三角形的角平分线、中线和高。 |
|||||
|
能力目标 |
培养学生的动手操作能力和学生的观察能力、识图能力。 |
||||||
|
情感目标 |
通过学生自己操作,加深对概念的理解,增强学生的自信心,提高学习数学的兴趣。 |
||||||
|
教学重点 |
三角形的角平分线、中线和高的概念及其画法 |
||||||
|
教学难点 |
钝角三角形的高的画法 |
||||||
|
教学形式 |
教学互动、学生自主探究、合作研讨 |
||||||
|
教具准备 |
投影仪辅助教学、三角板 |
||||||
|
教
学 过
程 |
|||||||
|
程序 |
教师活动 |
学生活动 |
设计意图 |
||||
|
一、 设境引入 |
做一做,议一议: 如图:将橡皮筋的一端固定在△ABC的顶点A上,另一端从点B出发沿BC移动到点C 观察哪些线段和角的大小发生了变化? (1)
(2) (4) 这节课我们就来研究三角形中一些特殊的线段 ------------高、角平分线和中线 |
动手操作 发现问题 |
通过图形的变换,让学生发现三角形中三条重要的线段,而这三条线与以前所学的垂线、角平分线及线段中点等概念有联系,从而达到知识迁移。 |
||||
|
二. 概念理解与应用 |
1 三角形的高: 如图,线段AD垂直BC,垂足为D,我们把线段 AD叫做△ABC 中BC边上的高 定义见教材P26 练习: (1)根据定义,你能画出△ABC 中AC边上的高 吗? (2)下列选项中,表示△ABC 中AB边上的高 是 ( ) (A)
(B)
(3)如图,分别画出下列三角形的高,观察各能画出几条?从中你发现了什么?
如图,线段AE平分∠BAC交边BC于点E,我们 把线段AE叫做△ABC 中∠BAC的角平分线 定义见教材P27 练习: (1)你能画出△ABC 中∠ABC的角平分吗? (2)用折纸的方法折出一张三角形纸片的角平分线,能折出几条?你有什么发现? 3 三角形的中线: 如图,F是△ABC边BC上的中点,我们把线段 AF叫做△ABC 中BC边上的中线 定义见教材 思考: (1) 如图,AF是△ABC 中BC边上的中线,则 ---------=-------- (2) △ABF与△BCF的面积之间有什么关系? (3) 如图,在△ABC 中,AD⊥BC于D,AD是BC 边上的---------,若AE=EC,BE是AC边上的--------,若∠1=∠2,CF是AB边上的----------
|
观察思考 合作探究 观察思考 合作探究 |
结合图形,了解三角形的三条重要线段, 观察、操作 加深对概念的理解与把握 |
||||
|
三 课堂小结 |
收获: 1 可以选择折纸或利用工具作出三角形的三种重要线段 2 三角形的三条高、三条角平分线及三条中线交于一点。 |
交流 体会 |
|
||||
|
四 布置作业 |
教材P28 习题4,5 |
|
|
||||
|
|
|
|
|
||||
7.4 认识三角形(一)
步骤一:学生小组讨论纸条长度的选择有哪些情况?
步骤二:学生动手操作,试一试自己找出的几种情况是否都能搭成三角形
步骤三:各小组总结本组观察、讨论后的结果:
三角形的任意两边之和大于第三边。
2 学会应用;
(1) 下列线段中,不能构成三角形的是 ( )
(A)2,4,5 (B)18,9,8
(C)6,8,8 (D)7,10,15
(2)以下列各组数据为边长,可以构成等腰三角形的是 ( )
(A)1cm、2cm、3cm (B)2cm、 2cm、 1cm
(C)1cm、3cm、1cm(D)2cm、 2cm、 5cm
(3)若等腰三角形的两边长分别是4,10,
则三角形的周长是___________
(4)有长度分别为2cm、 3cm、 4cm和5cm
的4根小木棒,任取其中3根,你可以搭出几种不同的三角形?
7.4 认识三角形(二)
|
课 题 |
7.4 认识三角形(二) |
课 型 |
新 授 课 |
||||
|
教 学 目 标 |
知识目标 |
通过学生动手操作,理解三角形的角平分线、中线和高等几个概念,并会正确画出任意一个三角形的角平分线、中线和高. |
|||||
|
能力目标 |
培养学生的动手操作能力和学生的观察能力、识图能力. |
||||||
|
情感目标 |
通过学生自己操作,加深对概念的理解,增强学生的自信心,提高学习数学的兴趣. |
||||||
|
教学重点 |
三角形的角平分线、中线和高的概念及其画法 |
||||||
|
教学难点 |
钝角三角形的高的画法 |
||||||
|
教学形式 |
教学互动、学生自主探究、合作研讨 |
||||||
|
教具准备 |
投影仪辅助教学、三角板 |
||||||
|
教 学 过 程 |
|||||||
|
程序 |
教师活动 |
学生活动 |
设计意图 |
||||
|
一、 设境引入 |
做一做,议一议: 如图:将橡皮筋的一端固定在△ABC的顶点A上,另一端从点B出发沿BC移动到点C 观察哪些线段和角的大小发生了变化? (1)
(2) (4) 这节课我们就来研究三角形中一些特殊的线段 ------------高、角平分线和中线 |
动手操作 发现问题 |
通过图形的变换,让学生发现三角形中三条重要的线段,而这三条线与以前所学的垂线、角平分线及线段中点等概念有联系,从而达到知识迁移. |
||||
|
二. 概念理解与应用 |
1 三角形的高: 如图,线段AD垂直BC,垂足为D,我们把线段 AD叫做△ABC 中BC边上的高 定义见教材P26 练习: (1)根据定义,你能画出△ABC 中AC边上的高 吗? (2)下列选项中,表示△ABC 中AB边上的高 是 ( ) (A)
(B)
(3)如图,分别画出下列三角形的高,观察各能画出几条?从中你发现了什么?
如图,线段AE平分∠BAC交边BC于点E,我们 把线段AE叫做△ABC 中∠BAC的角平分线 定义见教材P27 练习: (1)你能画出△ABC 中∠ABC的角平分吗? (2)用折纸的方法折出一张三角形纸片的角平分线,能折出几条?你有什么发现? 3 三角形的中线: 如图,F是△ABC边BC上的中点,我们把线段 AF叫做△ABC 中BC边上的中线 定义见教材 思考: (1) 如图,AF是△ABC 中BC边上的中线,则 ---------=-------- (2) △ABF与△BCF的面积之间有什么关系? (3) 如图,在△ABC 中,AD⊥BC于D,AD是BC 边上的---------,若AE=EC,BE是AC边上的--------,若∠1=∠2,CF是AB边上的----------
|
观察思考 合作探究 观察思考 合作探究 |
结合图形,了解三角形的三条重要线段, 观察、操作 加深对概念的理解与把握 |
||||
|
三 课堂小结 |
收获: 1 可以选择折纸或利用工具作出三角形的三种重要线段 2 三角形的三条高、三条角平分线及三条中线交于一点. |
交流 体会 |
|
||||
|
四 布置作业 |
教材P28 习题4,5 |
|
|
||||
|
|
|
|
|
||||
7.4 认识三角形(一)
步骤一:学生小组讨论纸条长度的选择有哪些情况?
步骤二:学生动手操作,试一试自己找出的几种情况是否都能搭成三角形
步骤三:各小组总结本组观察、讨论后的结果:
三角形的任意两边之和大于第三边.
2 学会应用;
(1) 下列线段中,不能构成三角形的是 ( )
(A)2,4,5 (B)18,9,8
(C)6,8,8 (D)7,10,15
(2)以下列各组数据为边长,可以构成等腰三角形的是 ( )
(A)1cm、2cm、3cm (B)2cm、 2cm、 1cm
(C)1cm、3cm、1cm(D)2cm、 2cm、 5cm
(3)若等腰三角形的两边长分别是4,10,
则三角形的周长是___________
(4)有长度分别为2cm、 3cm、 4cm和5cm
的4根小木棒,任取其中3根,你可以搭出几种不同的三角形?
1. 求不等式1-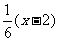 ≤
≤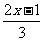 的最小整数解.
的最小整数解.
4.练习
课本P18练习1⑶⑷、2.
[例题设计]
例2解不等式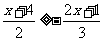 ,并把它的解集在数轴上表示出来。
,并把它的解集在数轴上表示出来。
补充例1. 求不等式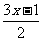 <3-
<3-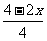 的正整数解.
的正整数解.
解:去分母:2(3x-1)≤12-(4-2x),?
去括号:6x-2≤12-4+2x,?
移项,合并同类项:4x≤10,?
系数化为1:x≤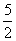 .?
.?
因为小于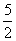 的正整数只有1和2,
的正整数只有1和2,
所以原不等式的正整数解是x=1或2.?
补充例2在“科学与艺术”知识竞赛的预选赛中共有20道题,对于每一道题,答对得10分,答错或不答扣5分,总得分不少于80分者通过预选赛.育才中学25名学生通过了预选赛,他们分别可能答对了多少道题?
(先让学生思考探索,再让学生充分发表自己的见解,最后教师引导指出解题方法)
提问:应用不等式解决实际问题的解题方法与步骤是什么?它与列方程解应用题有什么区别和联系?你能给予归纳吗?(由学生自己归纳)
解:设答对x道题,则答错或不答(20-x)道题.
根据题意:得10x-5(20-x)≥80,?
解得:x≥12.?
因为x为正整数,所以
?x=12、13、14、…、20.?
答:他们分别可能答对12,13,14,…,20道题,即至少应答对12道题.
[练习设计]
课内作业
课本P18练习1、2.
课后作业
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com