2.(河北省)两根木棒的长分别是7cm和10cm，要选择第三根木棒，将他们定成一个三角形框架，那么第三根木棒长x(cm)的范围是　　　 .

[点拨]应用三角形三边关系：两边之和大于第三边，两边之差小于第三边.

[答案]3<x<17

1.(吉林省)如图7-5-1，∠1+∠2+∠3+∠4=　 　　.

[点拨]两次应用三角形内角和是180⁰.

[答案]280⁰.

1.(聊城市)如图6-3-1是聊城市市区几个旅游景点的

示意图(图中每个小正方兴的边长为1个单位长度)，请以某景点为

原点，画出直角坐标系，并用坐标表示下列景点的位置：

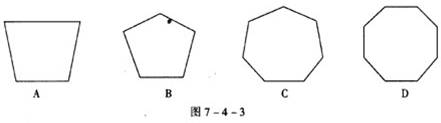
3.如图7-4-3所示的多边形中，能够铺满地面的是

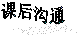
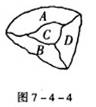如图7-4-4，下面是某市的地形图，其中4个图形(分别用A、B、C、D)表示，ABCD是一个不规则的平面密铺图形，你能不能用规则的三角形对他们进行加工，用三角形的密铺形式表示出来.

如图7-4-5，密铺地面的问题：单一式凸多边形组合，虽好却很简单，下面有一幅图片，你观后有何感想？

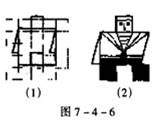　　 如图7-4-6，是一个制作幻灯片过程，图(1)是一个正方形的格子中画出轮廓，包正方形，三角形.图(2)是在这些轮廓上修饰.

　　 用白纸做8个试试，再把它们拼一拼，看能不能密铺平面

2.能搞铺满地面的正多边形组合是

　 A.正八边形和正方形　　　　　　　 B.正五边形和证十边形

C.正方形和正六边形　　　　 　　　D.正四边形和正七边形

1.若铺满地面的瓷砖每一个顶点出由6块相同的正多边形组成，此时的正多边形是(　 )

　　　 A.正三角形　　 B.正五边形　　　 C.正六边形　　 D.正八边形

3.如图7-4-2，分别指出下列图形组合是哪几种正多边形组合：

(a)　　　　　　 ;(b)　　　　　　 ;(c)　　　　　　 ;

(d)　　　　　　 ;(e)　　　　　　 ;(f)　　　　　　 ;

2.能用一种正多边形拼成地面的有　　　　 、　　　　 、　　　　 .

1.当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个　　　　 时，就拼成一个平面图形.

7.4 课题学习　 镶嵌

随着改革开放不断深入，中国的老百姓的居住条件发生了很大的变化，在装潢和装修房屋、美化生活中用到了许多正多边形的知识，怎么样学会设计巧妙地选用正多边形来拼图案呢，下面我们就一起进入奇特美妙的图形世界吧。

[例]用正五边形、正十边形这两种正多边形组合能否铺满平面？

[点拨]这两种正多边形能否铺满平面，一要看能否找到所取每个正多边形的一个内角的和恰好为一个周角；二要看几个相邻顶点都要被这两种正多边形组合成周角.

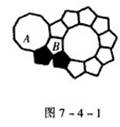[答案]因为正五边形的每个内角为108⁰，正是边形的每个

内角为144⁰，而108⁰×2+144⁰360⁰，所以经过一点(比如A)可由

两个正五边形，一个正式边形组成周角360⁰，如图7-4-1，所以

用正五边形、正十边形这两种正多边形组合不能铺满平面.