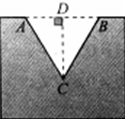
2、如图,工件上有一V型槽,测得它的上口宽20mm,深19.2mm.求V型角(∠ACB)的大小(结果精确到10 ).

练习：

已知sinA=0.9816，求锐角A，已知cosA＝0.8607，求锐角A；

已知tanA=0.1890，求锐角A；已知tanA＝56.78，求锐角A.

练习：根据下列条件求锐角θ的大小：

(1)tanθ＝2.9888；(2)sinθ=0.3957；(3)cosθ＝0.7850；(4)tanθ＝0.8972；

(5)sinθ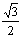＝；(6)cosθ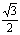＝； (7)tanθ=；

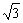经典例题：

1、如图,为了方便行人，市政府在10m高的天桥.两端修建了40m长的斜道.这条斜道的倾斜角是多少?

练习： (1)sin56°；(2)sin15°49′； (3)cos20°；(4)tan29°；

　　　 (5)tan44°59′59″；(6)sin15°+cos61°+tan76°.

判断下列等式是否成立？为什么？

(1)sin15°+sin25°＝sin40°(2)cos20°+cos26°=cos46°

(3)tan25°+tan15°＝tan40°

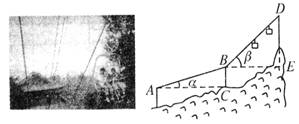
应用：如图，当登山缆车的吊箱经过点A到达点B时，它走过了200米，已知缆车行驶的路线与水平面的夹角为∠a＝16°，那么缆车垂直上升的距离是多少?

3、备选题：

　　 让学生设计一个由几个多边形镶嵌而成的优美的图案，并写上一两句贴切的解说词．

[教学反思]

本节课教学在上节课初步学习镶嵌的意义的基础上，继续深入探究由几个多边形镶嵌成平面图案的合理性，让学生通过对较熟悉的平面镶嵌图的探究，进而到对更复杂的平面镶嵌图的探究．最后让学生通过独立的观察、思考，并讨论、交流，归纳认识到数学问题的本质所在。在学生不断巩固数学知识的同时，使学生进一步体验数学源于生活又服务于生活的道理．

2、选做题：

　　 教科书97页习题l0。

1、必做题：

　　 画出若干个用两个或两个以上多边形镶嵌的图案．

2、可安排几分钟时间让学生自行设计一个或几个由几种多边形镶嵌而成的平面图案(也可以小组为单位合作完成)，并尝试让学生解释其合理性及象征性等。

设计意图：联系生活实际运用教学知识进行自我设计，叙述含义，使数学还原于生活。

1、让学生说说生活中见到的由几种多边形镶嵌而成的平面图案(或展示已画好、搜集到的其他图案)。

让学生思考问题:若干个多边形(常见的是正多边形)，能否组镶嵌成一个美丽的图案，关键是什么？

设计意图：通过对两个平面图案的观察、探索，结合本问题，让学生归纳、补充、了解到多种多边形的镶嵌关键，形成共识。

学生观察图7. 4-2书本93页)，围绕“图案由哪些多边形镶嵌而成”“为什么能出现这种结果”开展思考、讨论。

设计意图：深入探讨几种多边形组合而成的镶嵌问题，进一步理解并解释图案的合理性。