1．在下列直角三角形中不能求解的是　　　　　　　　　　　　　　　　　　　 (　 　　)

A、已知一直角边一锐角 ；B、已知一斜边一锐角；C、已知两边；D、已知两角

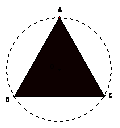
4、如图, ⊙O的半径为10,求⊙O的内接正三角形ABC的边长.

3、在Rt△ABC中,∠C=90°, ∠A-∠B=30°，a-b=2，解这个直角三角形.

2、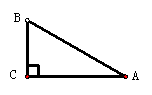在Rt△ABC中,∠C=90°,a=5,b=5.

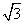　 求: (1)c的大小.　　 　　　　　　(2)∠A、∠B的大小.

定义：由直角三角形中的已知元素，求出所有未知元素的过程，叫做解直角三角形.

1、在Rt △ ABC中，∠C=90°，∠ A=30 °，a=5，求b、c的大小.

在Rt△ABC中,

(1)根据∠A= 75°,斜边AB=6,你能求出这个三角形的其他元素吗?

(2)根据AC=2.4m,斜边AB=6,你能求出这个三角形的其他元素吗?

(3)根据∠A=60°,∠B=30°,你能求出这个三角形的其他元素吗?

结论:在直角三角形的六个元素中,除直角外,如果知道　　 个元素(其中至少有一个是边),就可以求出其余三个元素.

思考:在Rt△ABC中，∠C为直角，其余5个元素之间有以下关系:

(1)三边之间的关系：　　　　　　　　　　

(2)锐角之间的关系：　　　　　　　　　　 　

(3)边角之间的关系：　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　

要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α一般要满足

50°≤ α ≤75°.现有一个长6m的梯子.问:

(1)使用这个梯子最高可以安全攀上多高的平房?(精确到0.1m)

(2)当梯子底端距离墙面2.4m时,梯子与地面所成的角α等于多少(精确到1°)?这时人能否安全使用这个梯子?

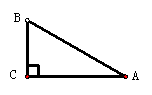星期天，小华去图书超市购书，因他所买书类在二楼，故他乘电梯

上楼，已知电梯倾斜角∠A=30°，则∠ B=　　　 °.

若电梯AC=8,BC=6,则AB= 　　　　；若电梯AC=8,BC=6, AB=10，则：

sinA=　　　 　，cosA= 　　　　，tanA=　　　 .

5．阳光中学校长准备在暑假带领该校的“市级三好生”去青岛旅游，甲旅行社说“如果校长买全票一张，则其余学生享受半价优惠.”乙旅行社说“包括校长在内，全体人员均按全票的6折优惠”.若到青岛的全票为1000元.

(1)　　　 设学生人数为x人，甲旅行社收费为y _甲元，乙旅行社收费为y_乙元，分别写出两家旅行社的收费表达式.

(2)就学生人数x，讨论哪家旅行社更优惠？

4.“中秋节”期间苹果很热销，一商家进了一批苹果，进价为每千克1.5元，销售中有6%的苹果损耗，商家把售价至少定为每kg多少元，才能避免亏本？