4．从上面的两道题可以看出，若知道两条边利用勾股定理就可以求出第三边，进而求出两个锐角，若知道一条边和一个锐角，可以.利用边角关系求出其他的边与角.所以，解直角三角形无非以下两种情况：

(1)已知两条边，求其他边和角.

(2)已知一条边和一个锐角，求其他边角.

3．例题讲解.

例1．如图，东西两炮台A、B相距2000米，同时发现入侵敌舰C，炮台A测得敌舰C在它的南偏东40°的方向，炮台B测得敌舰C在它的正南方，试求敌舰与两炮台的距离(精确到l米).

分析：本题中，已知条件是什么?(AB＝2000米，

∠CAB＝90°－ ∠CAD＝50°)，那么求AC的长是用

“弦”还是用“切”呢?求BC的长呢?显然，

AC是直角三角形的斜边，应该用余弦函数，

而求BC的长可以用正切函数，也可以用余切函数.

讲解后让学生思考以下问题：

(1)在求出后，能否用勾股定理求得BC；

(2)在这题中，是否可用正弦函数求AC，是否可以用余切函数求得BC.

通过这道例题的分析和挖掘，使学生明确在求解直角三角形时可以根据题目的具体条件选择不同的“工具”以达到目的.

2．解直角三角形的所需的工具.

(1)两锐角互余∠A+∠B＝90°

(2)三边满足勾股定理a²+b²＝c²

(3)边与角关系sinA＝cosB＝，cosA＝sinB＝，tanA＝cotB＝，cotA＝tanB＝.

1．解直角三角形的定义.

任何一个三角形都有六个元素，三条边、三个角，在直角三角形中，已知有一个角是直角，我们把利用已知的元素求出末知元素的过程，叫做解直角三角形.像上述的就是由两条直角边这两个元素，利用勾股定理求出斜边的长度，我们还可以利用直角三角形的边角关系求出两个锐角，像这样的过程，就是解直角三角形.

如图所示，一棵大树在一次强烈的台风中于地面10米处折断倒下，树顶落在离数根24米处.问大树在折断之前高多少米?　　

显然，我们可以利用勾股定理求出折断倒下的部分

的长度为＝26　 26+10＝36所以，

大树在折断之前的高为36米.

9、赞化学校有一块三角形形状的花圃ABC，现可直接测到∠A=30°，AC=40米，BC=25米，请你求出这块花圃可能的面积(结果保留根号).

8、如图，在四边形ABCD中，∠B=∠D=90°, ∠A=150°,AB=5,CD=15.求AD、BC长.

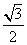7、在△ABC中，∠A=30°，tanB=，AC=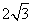，则AB=　　　　 .

6、已知在直角梯形ABCD中，上底CD=4，下底AB=10，非直角腰BC=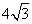，则底角∠B=　 　　°.

5、在Rt△ABC中，∠C=90°，AB=10cm，sinA=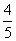，则BC的长为　　　 cm.