
3. 一木工有两根长分别为40厘米和60厘米的木条,要另找一根木条,钉成一个三角形木架. 问第三根木条的长度应在什么范围内?
2.填表:
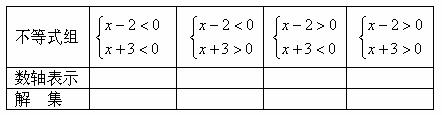
1. 解下列不等式组, 并把他们的解集在数轴上表示出来.
(1)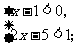 (2)
(2)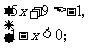
(3)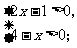 (4)
(4)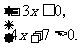
一元一次不等式组解集四种类型如下表:
不等式组(a<b |
数轴表示 |
解 集 |
记忆口诀 |
(1)  |
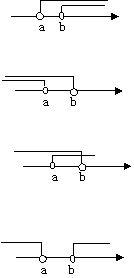 |
x>b |
同大取大 |
(2)  |
|
x<a |
同小取小 |
(3) 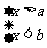 |
|
a<x<b |
大小取中 |
(4) 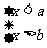 |
|
无解 |
矛盾无解 |
练习:课本P.26-练习1、2
例1 解不等式组

解 解不等式①, 得 .
解不等式②, 得 .
在同一数轴上表示不等式①、②的解集, 如图, 可知所求不等式组的解集是
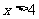 .
.


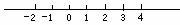
例2 解不等式组:

解 解不等式①,得 .
解不等式②, 得 .
在同一数轴上表示不等式①、②的解集, 如图可见, 这两个不等式的解集没有公共部分,这时,我们说这个不等式组 .

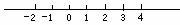
2.概念与方法:
不等式组中所有不等式的解集的公共部分叫做这个不等式组的解集.
求不等式组解集的过程叫做解不等式组.
方法:解一元一次不等式组, 通常可以先分别求出不等式中每一个不等式的解集, 再求出它们的公共部分. 利用数轴可以直观地帮助我们求出不等式组的解集.
1.问题的分析:
问: 求解应用题时,在很多情况下, 我们可以将某些适当的量设为未知数. 此题中我们如何来设元呢?
答:可以直接设元,设需要x分钟才能将污水抽完.
问:总的抽水量可表示成什么形式?
答:总的抽水量为 吨.
问:依据题中的条件,你能列出什么式子?
答:由题意,积存的污水在1200吨到1500吨之间,应有
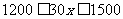 .
.
这实际上包括了两个不等式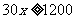 和
和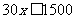 .
.


|
 再如课本:P.23
再如课本:P.23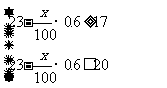
像这样,由几个含有同一个未知数的一次不等式组成的不等式组就叫做一元一次不等式组.

分别求这两个不等式的解集,得
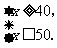
同时满足不等式①、②的未知数x应是这两个不等式解集的公共部分.
要求学生在同一数轴上表示这两个不等式的解集, 并找出公共部分.
如图, 公共部分是40和50之间的数(包括40和50), 记作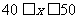 . 这就是所列不等式组的解集.
. 这就是所列不等式组的解集.

所提问题的答案为:大约需要40到50分钟能将污水抽完.
2.问题的提出:
用每分钟可抽30吨水的抽水机来抽污水管道里积存的污水, 估计积存的污水在1200吨到1500吨之间, 那么大约需要多少时间能将污水抽完?
1.什么叫做一元一次不等式?解一元一次不等式的一般步骤是什么?
3.一元一次不等式组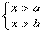 (
(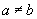 )的解集为
)的解集为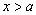 ,则
,则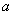 与
与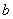 的大小关系为____________.
的大小关系为____________.
2 解不等式组:
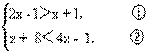
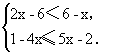
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com