2、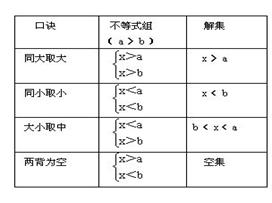巧用口诀确定一元一次不等式组的解集：

　[例题设计]

　例1 解不等式组：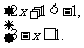

补充例题解不等式组：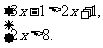

[练习设计]

课内作业

1、知识点小结：引导学生与老师、学生与学生讨论本节课所学的知识以及注意的地方。

课本第26页练习第1题．

例1 解不等式组：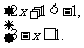

补充例题解不等式组：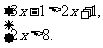

5. 概括总结

(1) 几个不等式的解集的公共部分，叫做由它们所组成的不等式组的解集．

(2) 解一元一次不等式组的方法

步骤：先求出不等式组中每一个不等式的解集，再求出它们的公共部分．找公共部分时，可以借助于数轴来帮助我们直观表示一元一次不等式组的解集．

4. 练习

让学生分别求出上面所列的不等式组中各个不等式的解集，并把各个解集在数轴上表示出来．

(让学生展开讨论，然后总结出不等式组的解集应为两个不等式解集的公共部分．这个解集可以通过数轴直观地表示出来)

3. 不等式组的解集

不等式组的解集应使不等式组中各个不等式都成立，因此不等式组的解集应是不等式组中各个不等式的解集的公共部分．

2. 导入一元一次不等式组的概念

由两个或两个以上的一元一次不等式合在一起，就得到了一个一元一次不等式组，如上面问题列出的?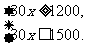

某种杜鹃花适宜生长在平均气温为17-20℃的山区，已知这一地区海拔每上升100m，气温下降0.6℃，现测出山脚下的平均气温是23℃.估计适宜种植这种杜鹃花的山坡的高度。

1. 参与其中，主动探究

分析上述问题的过程可以让学生自己来说，如果有的学生说不明白，可让其他学生补充，或者教师点拨、启发．

4．练习：课本P.28－习题1、2