
2、 声音在空气中的传播速度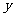 km/h(简称音速)与气温
km/h(简称音速)与气温
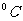 满足关系式:
满足关系式:
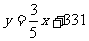 .求:
.求:
(1) 音速为340m/s时的气温。
(2) 音速超过340m/s时的气温。
(3) 你可以得到什么规律?说说看。
[设计说明]让学生在感受本节课的内容以后,验证自己所学习的知识,让孩子们快速的理解三个知识之间的关系。
补充例题:
一艘轮船以20km/h的速度从甲港驶往160km远的乙港,2h后,一艘快艇以40km/h的速度也从甲港驶往乙港。分别列出轮船和快艇行驶的路程y km与时间x h的函数关系式,并在直角坐标系中画出函数的图象,观察图象回答下列问题:
(1) 何时轮船行驶在快艇的前面?
(2) 何时快艇行驶在轮船的前面?
(3) 哪一艘船先驶过60km?哪一艘船先驶过100km?
[说明]本题可让学生自己回答问题,教师予以纠正。
总结思考
请回答一元一次不等式与一元一次方程、一次函数的内在联系。
练习巩固:
某学校计划购买若干台电脑,现从两家商场了解到同一型号电脑每台报价均为6000元,并且多买都有一定的优惠。甲商场的优惠条件是:第一台按原价收费,其余每台优惠25%;乙商场的优惠条件是:每台优惠20%。
(1) 分别写出两家商场的收费与所买电脑台数之间的关系式;
(2) 什么情况下到甲商场购买更优惠?
(3) 什么情况下到乙商场购买更优惠?
(4) 什么情况下两家商场的收费相同?
分析:究竟选择哪家商场购买电脑,可使费用最省,由题目的条件看,应由电脑的数量来确定,我们可以把问题转化为不等式,然后通过解不等式,使得问题迎刃而解,当然,也可以先讨论收费相同的情况,求得电脑的数量以后,再分析求解。
解:略
[设计思路]此题是一道方案决策最优化问题,但由于购买电脑的数量不确定,使得方案决策不确定,这就需要准确提取信息,通过列出代数式、找函数关系式、解不等式等数学手段,解决实际问题,应用不等式的知识解决日常生活问题是我们常见的题型。
作业:1、书本P32 习题7.7 1 2 3
1、 x取什么值时,函数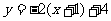 的值是正数?负数?非负数?
的值是正数?负数?非负数?
2、能否用一元一次方程和一次函数的性质来求解?
练习巩固
7.7一元一次不等式与一元一次方程、一次函数
[教学背景]在八年级上学期最后阶段,孩子们学习了一次函数以及一元一次方程,八下的前几节课学生们学习掌握了一元一次不等式的定义以及它的性质,会在坐标轴上表示表示不等式的解集。学到这里孩子们很自然的想到,一元一次不等式和上学期的知识有什么样的联系呢?本节课的内容将回答他们的疑惑。
[教学目标]其实生活中很多地方在遇到一元一次不等式的时候我们都是用一元一次方程来解决的,本节课以具体问题为载体,研究一元一次不等式与一元一次方程、一元一次函数的内在联系,揭示等与不等对立的双方在一定条件下可以互相转化。因此,我确定本节课的三维目标是:
[知识目标]通过比较一元一次方程和一元一次不等式的解题过程,让学生进一步体会解一元一次不等式与一元一次方程、一次函数之间的联系,了解他们的意义,使三个知识在这里形成一个交汇点,让孩子们了解数学知识的贯通性和关联性。
[能力目标]通过例题的学习,让学生拥有辨别一元一次不等式与一元一次方程、一次函数关系的能力,使得学生的知识能够形成网状结构,使知识能互相交融,培养触类旁通的能力,培养孩子们的发散思维。
[情感目标]三个知识在这里融合在一起了,孩子们的学习兴趣空前高涨,原来数学还可以这样学!孩子们会发现不同的知识其实也可以联系起来,培养孩子们辨证唯物看问题的观点,培养孩子们喜欢数学的情感,促进孩子们心理的成长。
教学情景
情景一、复习不等式的性质。
情景二、请同学们完成下面的问题:
已知: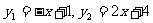 ,当
,当 取何植时,
取何植时,
(1)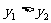 (2)
(2)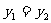 (3)
(3)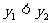
[设计思路]本题可以把问题转化为不等式和方程来求解或利用图象来求解,从而引出本节课要讨论的问题,过度自然。
情景三、一根长20CM的弹簧,一端固定,另一端挂物体.在弹簧伸长后的长度不超过30cm的限度内,每挂1kg质量的物体,弹簧伸长0.5cm,如果所挂物体的质量是x kg,弹簧的长度是ycm,求x于y之间的函数关系式,并画出函数的图像。
[设计思路]本题的综合性比较强,通过本题的训练很容易让孩子们找到三个知识的融汇点,通过比较增强他们的鉴别能力和自主学习的意识,这题所能达到的教学效果是老师“干”讲所达不到的,也就是“只可意会,不可言传”的境界,所以要多让孩子们自己完成。
分析:根据题意,这根弹簧挂xkg质量的物体后,伸长了0.5cm,此时弹簧的长度是(0.5x+20)cm,即得x与y之间得函数关系式
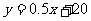
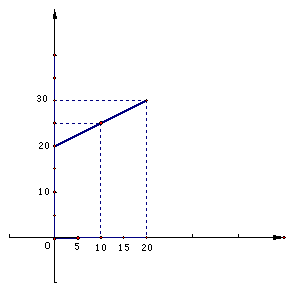 本题也可用图像法:
本题也可用图像法:
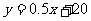
分析:因为所挂物体越重,弹簧伸得越长,又因为挂上物体后弹簧得长度不能超过30cm,所以当y=30时,该弹簧所挂物体得质量最大。
解一元一次方程
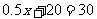
得
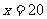
所以该弹簧所挂物体的最大质量是20kg.
问题:能否用不等式来求解?(请学生自由讨论)
注意:因为学生通过前面的学习很容易就能被这个题目所吸引,他们可能会安静的寻找答案,也可能会在一起讨论,那么我们不管发生什么情况一定要及时的予以辅导,要引导学生正确的找到不等关系,列出不等式,对于理解能力比较差的学生,教师可以单独辅导,也可以让先完成的同学讲解给后进生听,形成帮扶对子。最后一定要作总结给出正确的答案。
例题讲解
某人点燃一根长25cm的蜡烛,已知蜡烛每小时缩短5cm,社x h后蜡烛剩下的长度为y cm.
(1) 求y与x之间的函数关系式。
(2) 几小时后,蜡烛的长度不足10cm?
[设计说明]让学生自由发挥,给他们自己思考的空间,注意在这里一定要给孩子们充足的时间来考虑问题,不要草草了之,因为这个题目是孩子们大显身手的时间,孩子们需要这样的题目来检验自己学习的效果,体验成功的快感。最后的答案可能有很多种情况,但是一定要及时的评讲,要多给予鼓励。
解:(1)根据题意,得
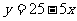
即y与x之间的函数关系为 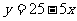
(2)当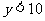 时
时
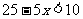
解这个不等式,得 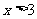
所以3小时后蜡烛的长度不足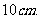
问题:1、你可以用其他方法解决这个问题吗?
10、哈尔滨市移动通讯公司开设了两种通讯业务:“全球通”使用者先缴50元月基础费,然后每通话1分钟,再付0.4元;“神州行”不缴月基础费,每通话1分钟,付话费0.6元(这里均指市内通话)。若一个内通话时间为x分钟,两种通讯方式的费用分别为y1元和y2元。
(1)写出y1,y2与x的关系式;
(2)一个月通话为多少分钟时,两种通讯方式的费用相同?
9、某汽车租赁公司要购买轿车和面包车共10辆,其中轿车至少要购买3辆,轿车每辆7万元,面包车每辆4万元,公司可投入的购车款不超过55万元;
(1)符合公司要求的购买方案有几种?请说明理由;
(2)如果每辆轿车的日租金为200元,每辆面包车的日租金为110元,假设新购买的这10辆车每日都可租出,要使这10辆车的日租金不低于1500元,那么应选择以上那种购买方案?
8、苏州地处太湖之滨,有丰富的水产养殖资源,水产养殖户李大爷准备进行大闸蟹与河虾的混合养殖,他了解到如下信息:
①每亩水面的年租金为500元,水面需按整数亩出租;
②每亩水面可在年初混合投放4公斤蟹苗和20公斤虾苗;
③每公斤蟹苗的价格为75元,其饲养费用为525元,当年可获1400元收益;
④每公斤虾苗的价格为15元,其饲养费用为85元,当年可获160元收益;
(1)若租用水面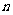 亩,则年租金共需__________元;
亩,则年租金共需__________元;
(2)水产养殖的成本包括水面年租金、苗种费用和饲养费用,求每亩水面蟹虾混合养殖的年利润(利润=收益-成本);
(3)李大爷现在资金25000元,他准备再向银行贷不超过25000元的款,用于蟹虾混合养殖。已知银行贷款的年利率为8%,试问李大爷应该租多少亩水面,并向银行贷款多少元,可使年利润超过35000元?
7、小杰到学校食堂买饭,看到A、B两窗口前面排队的人一样多(设为a人,a > 8),就站到A窗口队伍的后面. 过了2分钟,他发现A窗口每分钟有4人买了饭离开队伍,B窗口每分钟有6人买了饭离开队伍,且B窗口队伍后面每分钟增加5人.
(1)此时,若小杰继续在A窗口排队,则他到达窗口所花的时间是多少(用含a的代数式表示)?
(2)此时,若小杰迅速从A窗口队伍转移到B窗口队伍后面重新排队,且到达B窗口所花的时间比继续在A窗口排队到达A窗口所花的时间少,求a的取值范围(不考虑其他因素).
6、为了加快教学手段的现代化,某校计划购置一批电脑,已知甲公司的报价是每台5800元,优惠条件是购买10台以上,则从第11台开始按报价的70%计算;乙公司的报价也是每台5800元,优惠条件是每台均按报价的85%计算。假如你是学校有关方面负责人,在电脑品牌、质量、售后服务等完全相同的前提下,你如何选择?请说明理由?
5、(2007年河南省)某商场用36万元购进A、B两种商品,销售完后共获利6万元,其进价和售价如下表:
|
|
A |
B |
|
进价(元/件) |
1200 |
1000 |
|
售价(元/件) |
1380 |
1200 |
(注:获利=售价-进价)
(1) 该商场购进A、B两种商品各多少件?
(2) 商场第二次以原进价购进A、B两种商品.购进B种商品的件数不变,而购进A种商品的件数是第一次的2倍,A种商品按原价出售,而B种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于81600元,B种商品最低售价为每件多少元?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com