1.　　 什么叫因式分解？我们学过了什么样的因式分解的方法？

答：把一个多项式化成几个整式乘积形式，叫做把这个多项式因式分解；学过了提公因式法分解因式。

(11)(2003年上海市中考题)已知x²－2x=2,将下式先化简，再求值

(x－1)²+(x+3)(x－3)+(x－3)(x－1)

(8)(2x²+3y)(3y－2x²).

(9)(p－5)(p－2)(p+2)(p+5).

(10)(x²y+4)(x²y－4)－(x²y+2)·(x²y－3).

(4)(5x+3y)·(　　 )=25x²－9y²

(5)(－0.2x－0.4y)(　　 )=0.16y²－0.04x²

(6)(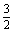－x－11y)(　　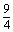 )=－x²+121y²

(7)若(－7m+A)(4n+B)=16n²－49m²,则A=　　　 ，B=　　　 .

(1) 在下列多项式的乘法中，不能用平方差公式计算的是(　　 )

A.(－a－b)(a－b)

B.(c²－d²)(d²+c²)

C.(x³－y³)(x³+y³)

D.(m－n)(－m+n)

(2) 用平方差公式计算(x－1)(x+1)(x²+1)结果正确的是(　　 )

A.x⁴－1　　　　　　　　　　　　　　　　　　　　　　　　　　 B.x⁴+1

C.(x－1)⁴　　　　　　　　　　　　　　　　　　　　　　　　　 D.(x+1)⁴

(3) 下列各式中，结果是a²－36b²的是(　　 )

A.(－6b+a)(－6b－a)

B.(－6b+a)(6b－a)

C.(a+4b)(a－4b)

D.(－6b－a)(6b－a)

2、某市电力公司为了鼓励居民用电，采用分段计费的方法计算电费：每月用电不超过100度，按每度0.57元计费；每月用电超过100度，前100度仍按原标准收费，超过部分按每度0.50元计费.

　(1)设月用x度电时，应交电费y元，当x≤100和x>100时，分别写出y (元)关于x (度)的函数关系式；

　(2)小王家第一季度交纳电费情况如下：

　问：小王家第一季度用电多少度？

1、某商场计划投入一笔资金采购一批紧销商品，经过市场调查发现，如果月初出售，可获利15%，并可用本和利再投资其他商品，到月末又可获利10%；如果月末出售，可获利30%，但要付出仓储费用700元，请根据商场情况，如何购销获利较多？

　(1)当自变量x的取值满足什么条件时，函数y=3x+8的值满足下列条件？　　①y=-7．　　　②y<2．

(2)　利用图象解出x：　　6x-4<3x+2．

　　 (3)A、B两个商场平时以同样价格出售相同的商品，在春节期间让利酬宾．A商场所有商品8折出售，B商场消费金额超过200元后，可在这家商场7折购物．试问如何选择商场来购物更经济．

(4)兄弟俩赛跑，哥哥先让弟弟跑9m，然后自己才开始跑。已知弟弟每秒跑3m，哥哥每秒跑4m。列出函数关系式，作出函数图象，观察图象回答下列问题：

(1)何时哥哥追上弟弟？

(2)何时弟弟跑在哥哥前面？

(3)何时哥哥跑在弟弟前面？

(4)谁先跑过20m？谁先跑过100m？

(1)1、一元一次方程与一次函数的关系

任何一元一次方程都可以转化为ax+b=0 (a, b为常数，a≠0)的形式，所以解一元一次方程可以转化为：当某个一次函数的值为0时，求相应的自变量的值.从图象上看，相当于已知直线y=ax+b确定它与x轴的交点的横坐标的值.

　(2)2、一次函数与一元一次不等式的关系

任何一个一元一次不等式都可以转化为ax+b>0或ax+b<0 (a, b为常数，a≠0)的形式，所以解一元一次不等式可以看作：当一次函数值大(小)于0时，求自变量的取值范围.

(3)3、规律总结

一次函数y=kx+b与一元一次方程kx+b=0和一元一次不等式的关系：函数y=kx+b的图象在x轴上的点所对应的自变量x的值，即为不等式kx+b>0的解集；在x轴上所对应的点的自变量的值即为方程kx+b=0的解；在x轴下方所对应的点的自变量的值即为不等式kx+b<0的解集.

例1：当自变量x为何值时函数y=2x-4的值大于0？

例2：　用画函数图象的方法解不等式5x+4<2x+10．

方法一：原不等式可以化为3x-6<0，画出直线_____________的图象，可以看出，当x_________________时这条直线上的点在x轴的下方．即这时y=3x-6<0，所以不等式的解集为：_______________

方法二：将原不等式的两边分别看作两个一次函数，画出直线________________与直线___________________可以看出，它们交点的横坐标为2．当x>2时，对于同一个x，直线_______________-上的点在直线_______________上的相应点的下方，这时5x+4<2x+10，所以不等式的解集为：_________________．

以上两种方法其实都是把解不等式转化为比较直线上点的位置的高低．

例3：求当自变量x取值范围为什么时，函数y=2x+6的值满足以下条件？

　　①y=0；　　②y>0．

例4：已知y₁=-x+3，y₂=3x-4，当x取何值时y₁>y₂？