
3.)用平方差公式分解因式的步骤:
(i)把二项差变成平方差的形式
 (ii)套公式
(ii)套公式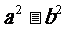 =
=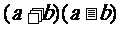 分解因式
分解因式
 (iii)整理化简到每个因式不能再分解为止。
(iii)整理化简到每个因式不能再分解为止。
 六、作业
六、作业
 课本22页习题8.2 A组1、2 。
课本22页习题8.2 A组1、2 。
2.)不是完全平方差的二项式不能用平方差公式来分解因式,例如 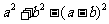 ,
, 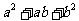 都不能用平方差公式来分解因式。
都不能用平方差公式来分解因式。
1.)多项式必须是二项式的形式且是两个完全平方的差,即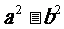 。
。
1.
用平方差公式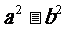 =
=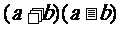 分解因式
分解因式
课本 17--18页练习1,2,3,4,(口答)
5 (1)(2)
3.得到 (2x+p+q)(p-q) 这两个因式的积,还要看每个因式用我们学过的方法,还能否分解因式? 如果不能,这道题算是完成了。
(2)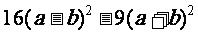
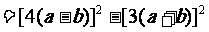
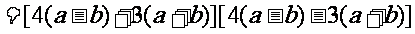
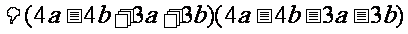

例题小结:通过例题可以看到,平方差公式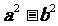 =(a+b)(a-b)中的a 和 b不仅表示数,同时也可以表示一个单项式或一个多项式。
=(a+b)(a-b)中的a 和 b不仅表示数,同时也可以表示一个单项式或一个多项式。
例1. 利用平方差公式分解因式。
(1)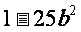 (2)
(2)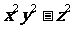
(3)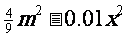
分析:利用平方差公式分解因式,必须把多项式变成公式的标准形式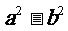 ,以上三题都不是标准形式,但看到
,以上三题都不是标准形式,但看到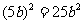 ,
,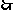
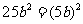 。同理
。同理 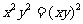 ,
,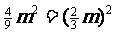 ,
,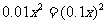 。
。
解:(1) 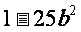 =
=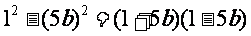
(2)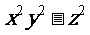 =
=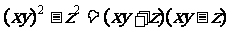
(3)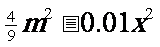
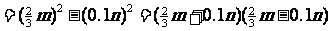
例2 把下列各式分解因式。
(1) 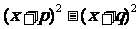
(2) 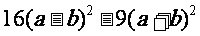
解: (1)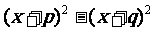 (这符合公式的标准形式)
(这符合公式的标准形式)
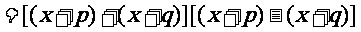
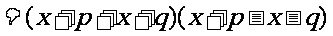
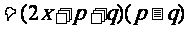
说明:1.这道题符合公式的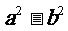 的标准形式,所以直接套公式,但公式里的a表示一个多项式(x+p), b 表示了另一个多项式(x+q) 套用公式时(x+p)和 (x+q) 都用小括号括起来。
的标准形式,所以直接套公式,但公式里的a表示一个多项式(x+p), b 表示了另一个多项式(x+q) 套用公式时(x+p)和 (x+q) 都用小括号括起来。
2. 分解因式后,每个因式里都有双重括号:中括号和小括号,所以每个因式里首先是按照法则去括号,得到(x+p+x+q)(x+p-x-q) ,看到每个括号内部都有同类项,要把同类项合并得到(2x+p+q)(p-q) 。
2.在整式乘法公式中学过(a+b)(a-b)= 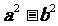 ,反过来就有
,反过来就有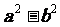 =(a+b)(a-b)。
=(a+b)(a-b)。
把多项式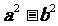 化为两个因式(a+b)和(a-b)的积的形式,这就是分解因式,这个公式就叫平方差公式。用这个公式,多项式
化为两个因式(a+b)和(a-b)的积的形式,这就是分解因式,这个公式就叫平方差公式。用这个公式,多项式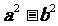 是可以分解因式的。
是可以分解因式的。
例如把多项式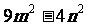 分解因式,它不能用提公因式法来分解,但
分解因式,它不能用提公因式法来分解,但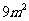 =
=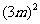 ,
,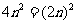 ,所以
,所以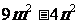 =
=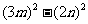 ,这是
,这是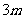 与
与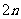 的平方差,所以能够用平方差公式来分解因式,即:
的平方差,所以能够用平方差公式来分解因式,即:
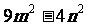 =
=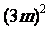
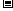
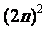 =(3m+2n)(3m-2n)
=(3m+2n)(3m-2n)
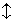
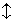
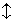
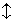
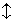
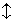
 =
= 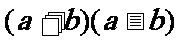
也就是说,任何一个多项式,只要能够化成平方差的形式,都可以套用平方差公式来 把这个多项式进行因式分解。
1. 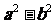 这样的多项式不能用提公因式法分解因式,它是否就不能分解因式呢?
不是的,今天要学种新方法--(出示课题)用平方差公式分解因式。
这样的多项式不能用提公因式法分解因式,它是否就不能分解因式呢?
不是的,今天要学种新方法--(出示课题)用平方差公式分解因式。
2. 什么样的多项式可以用提公因式法分解因式?
答:一个多项式的各项都含有相同的因式,就可以用提公因式法分解因式。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com