3．会判断一个分式何时有意义．

2．　 能用分式表示简单问题中数量之间的关系，能解释简单分式的实际背景或几何意义．

1．了解分式的概念，会判断一个代数式是否是分式。

8．1　分式

[教学目标]

6. 下列等式成立的是 [　 　]

　　 A.(a－b)²=a²－ab+b² 　　　　　B.(a+3b)²=a²+9b²

　　 C.(a+b)(a－b)=(b+a)(－b+a) 　　D. (x－9)(x+9)=x²－9

5. 若(x－y)²=0, 下面成立的等式是 [　 　]

　　 A.x²+y²=2xy 　　B.x²+y²=－2xy　　 　C.x²+y²=0 　　D.2x²－y²=0

4. 若(2a+3b)²=(2a－3b)²+( )成立, 则括号内的式子是 [　 　]

　　 A.6ab 　　B.24ab 　　C.12ab 　　D.18ab

2. (a－b)的平方等于(b－a)的平方．　　　　　　　　　　　 　( 　　)

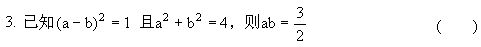
单选

1. (4x+3y)²=16x²+9y² 　(　 　)

4.在混合运算中，要注意运算的顺序.