
2、上述式子有什么共同的特点?
分式的概念:一般地,形如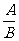 的式子叫做分式,其中A和B均为整式,B中含有字母.
的式子叫做分式,其中A和B均为整式,B中含有字母.
1、这些式子与分数有什么相同和不同之处?
3、两块面积分别为a ha、b ha的棉田,产棉花m㎏、n㎏.这两块棉田平均每公顷产棉花 ㎏.
思考
2、小丽用n元人民币买了m袋瓜子,那么每袋瓜子的价格是 元.
列出下列式子
1、一长方形的面积为2㎡,如果宽为am,那么长是 m.
京沪铁路是我国东部沿海地区纵贯南北的交通大动脉,全长1462km,是我国最繁忙的铁路干线之一.
如果货运列车的速度为akm/h,快速列车的速度为货运列车2倍,那么:
(1)货运列车从北京到上海需要多长时间?
(2)快速列车从北京到上海需要多长时间?
(3)已知从北京到上海快速列车比货运列车少用12h,你能列出一个方程吗?
3.例题教学
例1是为落实《标准》要求“能解释一些简单代数式的实际背景或几何意义”而设计,为解释简单分式的实际背景和几何意义而示范.
由于后续学习中多次涉及“不改变分式的值”,所以通过例2落实两个教学目标:什么是分式的值和如何求分式的值?什么是分式的值为0和何时分式的值为07例2虽是简单的数字计算,但应通过教学活动,让学生进一步感受分数与分式之间的关系--特殊与一般的辩证关系,即分式是一类分数的代表,只要给分式中的字母赋值,分式就是这一类分数中的一个特定分数,掌握赋值求值的方法.
分式何时有意义,何时无意义?是贯穿本章的基本问题,例3给出了判断方法.特别值得注意的是,为帮助学生弄清楚,为什么要探索分式何时有意义,但却从分式无意义着手?例3安排了两小问,旨在帮助学生搞清楚,使分母不等于0的值有无数个,而使分母等于0的值只有有限个.因此只要剔除这些使分母为0的值,分式就有意义了,用这种方法解决这一问题,只要解一个简单的方程,操作起来十分简便.这种“去杂”的思想方法是数学中一种很有价值的方法,教学重点是方法的分析而不是方法的操作.
可以根据学生的情况适当补充例题、习题,以帮助学生明确“分式的值为0”与“分式无意义”的区别,例如:当x是什么数时,分式 的值是0?
的值是0?
2.探索活动
(1)由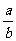 的意义,讨论
的意义,讨论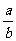 中的字母是否可以任意取值?由“分数的分母不能为0”,得到“分母b的值不能为0”的共识;
中的字母是否可以任意取值?由“分数的分母不能为0”,得到“分母b的值不能为0”的共识;
(2)通过对几个实际问题的研讨,学会用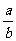 的形式表示实际问题中数量之间的关系,感受把分数推广到分式的优越性和必要性;
的形式表示实际问题中数量之间的关系,感受把分数推广到分式的优越性和必要性;
(3)关注 、
、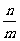 、
、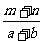 三式的共同点:
三式的共同点:
①都具有分数的形式;
②分母中都含有字母;
③分母中字母的取值要使分母不为0.
在概念教学过程中,应突出重点,注意层次:
(1)通过创设情境和探索活动,引入分式的概念已经水到渠成.课本采取排除干扰、突出本质的做法,淡化“分式是两个整式相除的商”的提法,直接给出分式的形式化定义和相关名称.
(2)为使学生正确认识分式的概念,课本通过与分数类比的方法,让学生明确:分式的分母不能为0;分式的分数线具有除号和括号的功能.
1.情境创设
(1)从问题情境人手,首先提问学生:分数与除法有什么关系?然后通过例题,帮助学生回顾两数相除得商表示为分数的过程;
(2)通过“用字母表示数”的方法,将上述过程转化为一般情况,即将a÷b表示为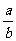 的形式.
的形式.
应引导学生注意上述转化的数学价值:用字母表示数,使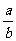 成为一类分数的代表;给字母赋予不同的数值,
成为一类分数的代表;给字母赋予不同的数值,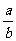 则为具体的分数.
则为具体的分数.
4.会根据已知条件求分式的值.
[教学过程]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com