
2.了解二元一次方程和二元一次方程组的解,会求二元一次方程的正整数解.
教学重点:
理解二元一次方程组的解的意义.
教学难点:
求二元一次方程的正整数解.
教学过程:
篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分.负一场得1分,某队为了争取较好的名次,想在全部22场比赛中得到40分,那么这个队胜负场数分别是多少?
思考:
这个问题中包含了哪些必须同时满足的条件?设胜的场数是x,负的场数是y,你能用方程把这些条件表示出来吗?
由问题知道,题中包含两个必须同时满足的条件:
胜的场数+负的场数=总场数,
胜场积分+负场积分=总积分.
这两个条件可以用方程
x+y=22
2x+y=40
表示.
上面两个方程中,每个方程都含有两个未知数(x和y),并且未知数的指数都是1,像这样的方程叫做二元一次方程.
把两个方程合在一起,写成
 x+y=22
x+y=22
2x+y=40
像这样,把两个二元一次方程合在一起,就组成了一个二元一次方程组.
探究:
满足方程①,且符合问题的实际意义的x、y的值有哪些?把它们填入表中.
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
上表中哪对x、y的值还满足方程②
一般地,使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解.
二元一次方程组的两个方程的公共解,叫做二元一次方程组的解.
例1 (1)方程(a+2)x +(b-1)y = 3是二元一次方程,试求a、b的取值范围.
(2)方程x∣a∣ – 1+(a-2)y = 2是二元一次方程,试求a的值.
例2 若方程x2 m –1 + 5y3n – 2 = 7是二元一次方程.求m、n的值
例3 已知下列三对值:
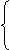
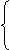
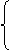 x=-6 x=10 x=10
x=-6 x=10 x=10
y=-9 y=-6 y=-1
(1)
|
 哪几对数值使方程
哪几对数值使方程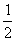 x-y=6的左、右两边的值相等?
x-y=6的左、右两边的值相等?
(2) 哪几对数值是方程组 的解?
例4 求二元一次方程3x+2y=19的正整数解.
课堂练习:
教科书第102页练习
习题8.1 1、2题
作业:
教科书第102页3、4、5题
1.认识二元一次方程和二元一次方程组.
8.1二元一次方程组
教学目标:
8.1分式 练习题
|
一、填空: 1、梯形的中位线长为m,面积为S,则它的高为 ; 2、在分式 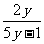 中,当y= 时,分式没有意义;当y= 时,分式值为0; 中,当y= 时,分式没有意义;当y= 时,分式值为0;3、当x= 时,分式 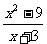 的值为0; 的值为0;4、某工厂原计划a天完成b件产品,若现在需要提前x天完成,则现在每天要比原来多生产产品__________ 件; 5、在分式 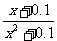 中,当x为
时,分式有意义;当x= 时,分式值为0 中,当x为
时,分式有意义;当x= 时,分式值为0二、选择: 1、下列各式中,是分式的是 ( ) A.2+ 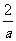 B.
B. 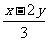 C. C.  D. D.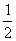 (a+b) (a+b) 2、若分式有意义,则 ( ) A.x≠2 B.x≠-1 C.x≠-1且x≠2 D.x>2 3、无论x取什么值,下列分式总有意义的是 ( ) A. 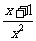 B.
B. 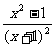 C . C . 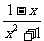 D. D.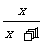 . .4.当x=- 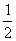 时,下列分式中有意义的是
( ) 时,下列分式中有意义的是
( )A. 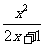 B. B. C. C. 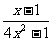 D.
D.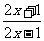 5.如果分式  的值为1,则x的值为
( ) 的值为1,则x的值为
( )A.x≥0 B.x>3 C.x≥0且x≠3 D. x≠3 三、解答题: 1.当x取什么数时,下列分式有意义? ①. 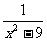 ②.
②.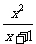 ③.
③. |
2.当x=2时分式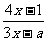 没有意义,求a 没有意义,求a 3.求下列分式的值: ① 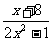 ,其中x=- ,其中x=-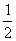 ②
②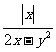 ,其中x=-1,y=- ,其中x=-1,y=-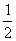  4.①已知分式 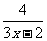 的值为正,求x的取值范围 的值为正,求x的取值范围②在代数式 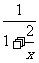 中,求实数x的取值范围 中,求实数x的取值范围拓展提高: 1.是否存在x的值,使得当a=2时,分式 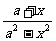 的值为0 的值为02.当x取何整数时,分式 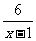 的值是整数? 的值是整数? |
5、请你举例说明分式 的实际意义
的实际意义
4、
当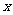 取什么值时,下列分式有意义?
取什么值时,下列分式有意义?

 (1)
(1)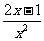 (2)
(2)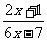 (3)
(3)
3、 求下列分式的值:
 (1)
(1)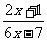 ,其中
,其中 ; (2)
; (2)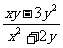 ,其中
,其中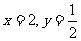
2、 用a kg橘子糖、b kg椰子糖、c kg奶糖混合成“什锦糖”,如果这3种糖
的单价分别是:28元/kg、32元/kg、48元/kg,那么这种“什锦糖”的单价是
元/kg。
|
教 学 过 程 |
集体讨论 |
|
一、情景设计 由1÷2、-3÷4可以表示成分数 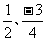 ,类比:用字母 ,类比:用字母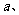 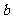 分别表示分数的分子和分母,那么 分别表示分数的分子和分母,那么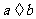 可以表示成 可以表示成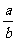 ,这种式子可以叫什么式子?(引出课题) ,这种式子可以叫什么式子?(引出课题)二、探索活动 1、用分数线的形式分别表示课本第40页中3个情景中数量之间的关系,找出 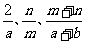 等式子的共同点,它们与分数的相同和不同之处。 等式子的共同点,它们与分数的相同和不同之处。2、引导学生归纳分式概念,并由分数知识引导学生分析出: (1)分式中分数线具有除号和括号功能; (2)分式的分母不能为0。 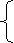 (3) 有理式 整式 (3) 有理式 整式 分式 3、由学生自己写几个分式,师再写几个代数式让学生找出其中哪些是分式 三、例题教学 1、课本第41页例1(引导学生用其它实际背景或几何意义说明) 2、课本第41页例2 (与代数式的值相比较,使学生理解分式的值是指其中字母用具体数值代替时的值) |
|
|
教 学 过 程 |
集体讨论 |
|
3、课本第42页例3 (与分数类比,说明分式有、无意义也是看分式的分母是否为0) 4、课本第42--43页练习1、2、3 四、思维拓展 1、当 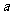 取什么值时,分式 取什么值时,分式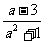 的值是正数 ? 的值是正数 ?2、一工程甲工程队单独做需要a天完成,乙工程队单独做需要b天完成,如果2队合做,需要多少天完成? 3、 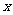 取什么值时,分式 取什么值时,分式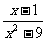 (1)无意义;(2)有意义 (1)无意义;(2)有意义五、总结 1、 写出几个分式; 2、 分式有、无意义的条件。 六、板书设计 七、教学反思 |
|
随堂练习13: 8.1 分 式
班级 学号 姓名 成绩
1、 某玩具厂要加工x只2008奥运吉祥物“福娃”,原计划每天生产y只,实际每天生产(y+z)只,
(1)该厂原计划 天完成任务(2)该厂实际用 天完成任务
教学难点:分式有、无意义的条件
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com