
5.(我国古代问题)有大小两种盛酒的桶,已经知道5个大桶加上1个小桶可以盛酒3斛(斛,音hu是古代的一种容量单位),1个大桶加上5个小桶可以盛酒2斛。1个大桶、1个小桶分别可以盛酒多少斛?
答案:设1个大桶可盛酒x斛、1个小桶分别可以盛酒y斛。
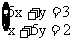
解得

4.用1块A型钢板可制成2块C型钢板,1块D型钢板;用1块B型钢板可制成1块C型钢板,2块D型钢板。现需15块C型钢板,18块D型钢板,可恰好用A型钢板,B型钢板各多少块?
答案:设用x块A型钢板,用y块B型钢板。
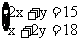
解得
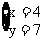
3.1号仓库与2号仓库共存粮450吨,现从1号仓库运出存粮的60%,从2号仓库运出存粮的40%,结果2号仓库所余的粮食比1号仓库所余的粮食多30吨。1号仓库与2号仓库原来各存粮多少吨?
答案:设1号仓库存粮x吨,2号仓库存粮y吨。
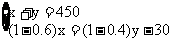
解得
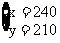
2.
分别用代入消元法、加减消元法求出它的解来。
答案: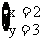
1.2x-5y=18
找学生写出它的五个解。
通过提问学生一些相关问题,引导总结总结出本节的知识点,形成以下的知识网络结构图。
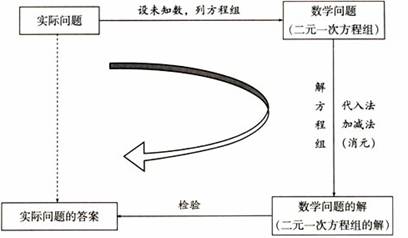
本章含有两个主要思想:消元和方程思想。所谓方程思想是指在求解数学问题时,从题中的已知量和未知量之间的数量关系人手,找出相等关系,运用数学符号形成的语言将相等关系转化为方程(或方程组),再通过解方程(组)使问题获得解决,方程思想是中学数学中非常重要的数学思想方法之一,它的应用十分广泛。
前面已学过二元一次方程组及一次方程组的应用题,这一节课主要把这一部分内容小结一下,并加以巩固练习。
2.了解二元一次方程和二元一次方程组的解,会求二元一次方程的正整数解.
教学重点:
理解二元一次方程组的解的意义.
教学难点:
求二元一次方程的正整数解.
教学过程:
篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分.负一场得1分,某队为了争取较好的名次,想在全部22场比赛中得到40分,那么这个队胜负场数分别是多少?
思考:
这个问题中包含了哪些必须同时满足的条件?设胜的场数是x,负的场数是y,你能用方程把这些条件表示出来吗?
由问题知道,题中包含两个必须同时满足的条件:
胜的场数+负的场数=总场数,
胜场积分+负场积分=总积分.
这两个条件可以用方程
x+y=22
2x+y=40
表示.
上面两个方程中,每个方程都含有两个未知数(x和y),并且未知数的指数都是1,像这样的方程叫做二元一次方程.
把两个方程合在一起,写成
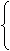 x+y=22
x+y=22
2x+y=40
像这样,把两个二元一次方程合在一起,就组成了一个二元一次方程组.
探究:
满足方程①,且符合问题的实际意义的x、y的值有哪些?把它们填入表中.
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
上表中哪对x、y的值还满足方程②
一般地,使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解.
二元一次方程组的两个方程的公共解,叫做二元一次方程组的解.
例1 (1)方程(a+2)x +(b-1)y = 3是二元一次方程,试求a、b的取值范围.
(2)方程x∣a∣ – 1+(a-2)y = 2是二元一次方程,试求a的值.
例2 若方程x2 m –1 + 5y3n – 2 = 7是二元一次方程.求m、n的值
例3 已知下列三对值:


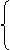 x=-6 x=10 x=10
x=-6 x=10 x=10
y=-9 y=-6 y=-1
(1)
|
 哪几对数值使方程
哪几对数值使方程 x-y=6的左、右两边的值相等?
x-y=6的左、右两边的值相等?
(2) 哪几对数值是方程组 的解?
例4 求二元一次方程3x+2y=19的正整数解.
课堂练习:
教科书第102页练习
习题8.1 1、2题
作业:
教科书第102页3、4、5题
1.认识二元一次方程和二元一次方程组.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com