
探究[5]
满足方程①,且符合实际的意义的x,y的值有那些?把它们填入表中。
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
上表中哪对x,y的值还满足方程②?
5]设计这个探究的目的是,让学生通过对具体数值代人方程的过程,感受到满足一个二元一次方程的未知数的值有许多对。由于要考虑实际意义,所以满足方程①的未知数的值有23对(未知数为0-22的整数)。
由上表可知,x=0,y=22;x=1,y=21……x=22,y=0使方程x+y=22两边的值相等,它们是方程x+y=22的解。如果不考虑方程x+y=22与上面实际问题的联系,那么x=-1,y=23;x=0.5,y=21.5……也都是这个方程的解。一般地,使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解。[6]
4]这里给出二元一次方程组的概念,两个二元一次方程合在一起就组成二元一次方程组。更一般地说,如果两个一次方程合起来共有两个未知数,那么它们组成一个二元一次方程组。特别地,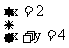 ,和
,和 这样的方程组也是二元一次方程组。
这样的方程组也是二元一次方程组。
小练习:已知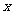 、
、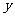 都是未知数,判别下列方程组是否为二元一次方程组?
都是未知数,判别下列方程组是否为二元一次方程组?
①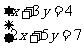 ②
②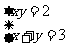
③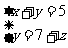 ④
④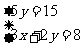
3]由于问题中包含两个必须同时满足的条件(等量关系),所以未知数x,y必须同时满足方程 ①,②,也就是说,我们要解出的x,y必须是这两个方程的公共解。
像这样,把两个二元一次方程合在一起,就组成了一个二元一次方程组[4] (system of linear equations of two unknowns)。
2.二元一次方程的左边和右边都应是整式
我们已经知道了什么是二元一次方程,下面完成练习。
判断下列方程是否为二元一次方程,并说明理由。
①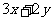 ②
②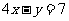 ③
③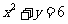
④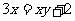 ⑤
⑤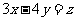 ⑥
⑥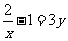
上面的问题中包含两个必须同时满足的条件[3],也就是未知数x、y必须同时满足方程
x+y=22 ①
和
2x+y=40。 ②
把这两个方程合在一起,写成
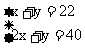
1.定义中未知数的项的次数是1,而不是指两个未知数的次数都是1
2]这是二元一次方程的定义,它是根据方程的形式,特别是其中未知数的形式给出的,可以对照一元一次方程的定义,理解这种定义方式以及两种方程的区别与联系。
注意:
我们来看一个问题:
篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分。某队为了争取较好名次想在全部22场比赛中得到40分,那么这个队胜负场数应分别是多少?
思考:
以上问题包含了哪些必须同时满足的条件?设胜的场数是x,负的场数是y,你能用方程把这些条件表示出来吗?
由问题知道,题中包含两个必须同时满足的条件:[1]
1]这里所说的条件,是等量关系。下面的文字所组成的等式和方程,以不同形式表达了问题中的两个等量关系,而这两个等量关系是同时成立的。
胜的场数+负的场数=总场数,
胜场积分+负场积分=总积分,
这两个条件可以用方程
x+y=22,
2x+y=40
表示。
上面两个方程中,每个方程都含有两个未知数(x和y),并且未知数的指数都是1,像这样的方程叫做二元一次方程[2] (1inear equation Of two unknowns)。
这两个方程有什么特点?与一元一次方程有什么不同?
(1)什么叫方程?什么叫方程的解和解方程?你能举一个一元一次方程的例子吗?
回答老师提出的问题并自由举例。
学生头脑中再现有关一元一次方程的知识,为学习二元一次方程做铺垫。
|
小结与复习 知识结构图 练习 |
引导学生总结本节的知识点。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com