
2、必须同时满足两个方程。
这题的胜5场平1场就是方程组的解
上题中方程组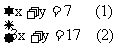 的解就是
的解就是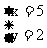
1、二元一次方程组的解是一对数,而不是两个数,必须用“ 来表示
来表示
3、二元一次方程组的有关定义
问:上面所列方程各含有几个未知数? 2个未知数
含有未知数的项的次数是多少? 次数是1
定义:含有两个未知数,并且所含未知数的项的次数都是 1 的方程叫做二元一次方程.
课内练习:比一比看谁快
(1) x+y+z=9 (2) x=6
(3) 2x+6y=14 (4) xy+y=7
(5) 7x+6y+4=16 (6) x²+y=6
议一议
问:方程 x+y=7 和 x+3y=17中,x的含义相同吗?y呢?
定义:把这两个二元一次方程合在一起,就组成了一个二元一次方程组.
(方程组各方程中同一字母必须代表同一个量)
定义:满足一个二元一次方程的每一对未知数的值,叫做这个二元一次方程的一个解
例如 x=3,y=4就是方程 x+y=7的一个解,我们把它记作: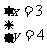
二元一次方程的解有无数个。
问:其他有没有了呢?
定义:一般地,使二元一次方程组的两个方程左右两边的值相等的两个未知数的值,叫做二元一次方程组的解。
2、列表:
设勇士队胜了x场,平了y场,那么根据填表的结果可知
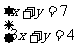
1、提出问题1: 暑假里,《新晚报》组织了“我们的小世界杯”足球邀请赛。勇士队在第一轮比赛中共赛9场,得17分。
比赛规定胜一场得3分,平一场得1分,负一场得0分。勇士队在这一轮中只负了2场,那么这个队胜了几场?又平了几场呢?
问:那么一般足球联赛的得分规则是什么呢?(请爱好足球的学生回答)
胜一场得3分,平一场得1分,负一场得0分。
n 甲队胜2场,平2场,负一场,那么甲队共赛几场?得几分?
n 甲队共赛5场,胜3场,负一场,那么甲队平了几场?又得了几分?
n 甲队共赛9场,得17分,负2场,那么甲队胜了几场,又平了几场?(胜5场,平场)
8.2幂的乘方与积的乘方(2)
|
课 题 |
第八章 幂的运算 |
课时分配 |
本课(章节)需
课时 本 节 课 为 第 课时 为 本 学期总第 课时 |
|||||
|
8.2幂的乘方与积的乘方(2) |
||||||||
|
教学目标 |
1.掌握积的乘方法则,并会用它熟练进行运算。 2.会双向应用积的乘方公式。 3.会区分积的乘方,幂的乘方和同底数幂乘法。 |
|||||||
|
重 点 |
1.掌握积的乘方法则,并会用它熟练进行运算。 2.积的乘方法则的推导过程。 |
|||||||
|
难 点 |
会双向运用积的乘方公式,培养学生“以理驭算”的良好运算习惯。 |
|||||||
|
教学方法 |
讲练结合、探索交流 |
课型 |
新授课 |
教具 |
投影仪 |
|||
|
教 师 活 动 |
学 生 活 动 |
|||||||
|
一.复习提问: 1.同底数幂的乘法法则 (1)语言表达, (2)式子表示。 2.幂的运算法则 (1)语言表达, (2)式子表示。 3.上两节课备用题选几道板演 二.新课讲解: 1.做一做 P54  (1)(3×2)3 =
, (1)(3×2)3 =
, 32×23=
。 32×23=
。 (2)[3×(-2)]3 =
, (2)[3×(-2)]3 =
, 32×(-2)3= 。 32×(-2)3= 。 (3)(1/3×1/2)3 = , (3)(1/3×1/2)3 = , (1/3)2×(1/2)3=
。 (1/3)2×(1/2)3=
。换几个数试试,并且同学之间互相交流。 问:你发现了什么规律? 要求学生根据结果发现规律。 2.法则的推导 当n是正整数时,    (ab)n =(ab)·(ab)·﹒﹒﹒·(ab) (ab)n =(ab)·(ab)·﹒﹒﹒·(ab)n个ab     =(a﹒a·﹒﹒﹒·a)·(b﹒b·﹒﹒﹒·b) =(a﹒a·﹒﹒﹒·a)·(b﹒b·﹒﹒﹒·b)  n个a
n个b
n个a
n个b=anbn 所以(ab)n =anbn (n是正整数) 学生口述:积的乘方,把积的每一个因式分别乘方,再把所得的幂相乘。 3.例题解析 P55 例1:题略 注意:(1)5 的三次方不能漏算。 (2)注意符号。 议一议:当n是正整数时,(abc)n =an·bn· cn 成立吗? 法则的推而广之: 当n是正整数时,(abc)n =an·bn ·cn 例2:题略 说明:是(abc)n =an·bn ·cn 的活用。 4.练一练:P55 题1:学生板演。 题2:学生口答并说明理由。 题3、题4:师生互动。 5.小结:本节课我们学习了积的乘方的运算法则,望同学们在用此法则时不要同同底数幂的运算法则和幂的乘方的运算混淆了。 教学素材: A组题:  (1) [(-2)×106]2·[(6×102)2 = (1) [(-2)×106]2·[(6×102)2 =   (2) 若 (a2 bn)m
=a4·b6 ,则m = n = (2) 若 (a2 bn)m
=a4·b6 ,则m = n = (3) (-1/7)8 ·494= (3) (-1/7)8 ·494= (4) 0.52004·22004= (4) 0.52004·22004= (5)(-x)2·x·(-2y)3 +(2xy)2·(-x)3 ·y = (5)(-x)2·x·(-2y)3 +(2xy)2·(-x)3 ·y =B组题:  (1)若 xn=5 , yn=3 则 (xy)2n= (1)若 xn=5 , yn=3 则 (xy)2n= (2) (-8)2003·0.1252002= (2) (-8)2003·0.1252002= |
学生回答 由学生自己先做(或互相讨论),然后回答,若有答不全的,教师(或其他学生)补充. 学生板演 |
|||||||
|
作业 |
第56页第1(4)(5)(6)、3(2)、4、5题 |
|||||||
|
板 书
设 计 |
||||||||
|
复习 例1
板演 …… …… …… …… …… …… …… 例2 …… …… …… …… …… …… …… |
||||||||
|
教 学
后 记 |
||||||||
|
|
||||||||
8.2幂的乘方与积的乘方(1)
|
课 题 |
第八章 幂的运算 |
课时分配 |
本课(章节)需
课时 本 节 课 为 第 课时 为 本 学期总第 课时 |
|||||
|
8.2幂的乘方与积的乘方(1) |
||||||||
|
教学目标 |
1.掌握幂的乘方法则,并会用它熟练进行运算。 2.会双向应用幂的乘方公式。 3.会区分幂的乘方和同底数幂乘法。 |
|||||||
|
重 点 |
1.掌握幂的乘方法则,并会用它熟练进行运算。 2.幂的乘方法则的推导过程。 |
|||||||
|
难 点 |
会双向运用幂的乘方公式,培养学生思维的灵活性。 |
|||||||
|
教学方法 |
讲练结合、探索交流 |
课型 |
新授课 |
教具 |
投影仪 |
|||
|
教 师 活 动 |
学 生 活 动 |
|||||||
|
一.情景设置: 问题1:哪位同学能在黑板上写下100 个104 的乘积? 经过试验,同学们会发现黑板上写不下1。 问题2:那哪位同学能用一个比较简单的式子表示100个104 的乘积? 根据乘方的定义,100 个104 的乘积不就是(104)100 吗? 板书:幂的乘方 二.新课讲解: 1.做一做 P52 计算下列各式:  ⑴ (23)2 = ⑴ (23)2 = ⑵ (a4)3 = ⑵ (a4)3 = ⑶ (am)5 = ⑶ (am)5 =问题:从上面的计算中,你发现了什么规律? 分析:让学生回到定义中去,进而在由同底数幂的乘法法则得出结果,比较后易找找规律。 当m 、n是正整数时,   (am)n =am ﹒am ﹒ ...﹒ am (am)n =am ﹒am ﹒ ...﹒ am n个am
n个am   =am+m+...+m
=am+m+...+mn个m =amn 所以(am)n =amn (m 、n是正整数) 学生口述:幂的乘方,底数不变,指数相乘。 3.例题解析 P53 例1:题略 分析:⑴ 直接运用法则。 ⑵ 4m 数字在前,字母在后。 ⑶ 注意“-” ⑷ 负数的几次幂是负数 例2:题略 分析:本课的难点,要求学生仔细辨析,何时用同底数幂的法则,何时用幂的乘方法则,何时是合并同类项,不可张冠李戴。 例3:题略 说明:应用题要写答案,最后用科学记数法。 4.练一练: P54 师生互动,及时点评。 5.小结:本节课我们学习了幂的乘方的运算法则,望同学们在用此法则时不要同同底数幂的运算法则混淆了。 教学素材: A组题: ⑴ a12 =(a3)( ) =(a2)( )=a3 a( ) =( )3 =( )4 ⑵ 32﹒9m =3( )  ⑶ y3n =3, y9n
= ⑶ y3n =3, y9n
=  ⑷ (a2)m+1 = ⑷ (a2)m+1 =⑸ {(a-b)3 } 2=(b-a )( ) B组题:  ⑴ 4﹒8m﹒16m =29 m= ⑴ 4﹒8m﹒16m =29 m= ⑵ 如果 2a=3 ,2b=6 ,2c=12, 那么 a、b、c的关系是 ⑵ 如果 2a=3 ,2b=6 ,2c=12, 那么 a、b、c的关系是
|
学生回答 由学生自己先做(或互相讨论),然后回答,若有答不全的,教师(或其他学生)补充. 学生板演 |
|||||||
|
作业 |
第56页第1(1)(2)(3)、2(1)(2)(3)(4)、3(1)题 |
|||||||
|
板 书
设 计 |
||||||||
|
复习
例1
板演 …… …… …… …… …… …… …… 例2 …… …… …… …… …… …… …… |
||||||||
|
教 学
后 记 |
||||||||
|
|
||||||||
恳请评委老师多多批评指正!
分层作业的设计满足学生多样性的学习需求,符合因材施教的原则。使我们的教学真正做到面向全体。
总之,在整个教学过程中,我充分发挥了学生的主体作用,新知识是通过学生自主探索,在合作交流过程中获得的。教师在过程中扮演了参与者、合作者、引导者、启迪者的角色,充分体现了新课标的教学理念。
我的教学过程中也有不足之处:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com