
4.如果∠DBE= ,那么DA//EB。( )
3.若∠A+∠ABE=180度,则 // ( )
2.若∠DBE=∠E,则 // ( )
教师展示例题,提出问题:
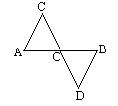
问题3.找出图中互相平行的直线,说明理由。

学生独立完成,并说明理由。(通过学生对此题的几种识别方法的说明,进一步熟悉三种识别方法。学生思考回答,教师评价学生的方法,及时给予肯定。)
问题4.如图:





 D
D
E
A B C
1.若∠A=∠EBC,则 // ( )
问题2:
请同学们动手做一做--用三根木条做一个实验。
 如图:移动AB(绕点G),当∠EGM与∠EHM具有怎样的关系时,AB//CD呢?
如图:移动AB(绕点G),当∠EGM与∠EHM具有怎样的关系时,AB//CD呢?
 A
E
A
E
G
 C H
D M
C H
D M
F
学生用三根木条,摆成如图的形状,移动AB(绕点G)。观察:随着∠EGM的度数改变,直线AB与CD的位置关系有什么变化?再移动CD试试?
(说明:学生动手操作,参与数学的学习活动。学生经过探索可以得出:当∠EGM=∠EHM时,AB//CD。并用语言叙述“同位角相等,两直线平行”。)
教师利用几何画板中的功能,分别演示同位角、内错角与同旁内角变化时,直线AB与CD的位置变化情况。
教师结合实际生活中有需要判断直线平行的具体实例,提出问题:
问题1:
让学生观察:实际生活中随处可见的道路、房屋、山川、桥梁……在这些大自然的杰作和人类的创造物中蕴含着大量的平行关系,你能从这些图片(电脑展示宏伟建筑:体育活动课中的双杠、铁轨、桥梁等)中找出互相平行的直线吗?请同学们也展示一下自己收集的图片,互相说说有哪些平行关系?
学生观察,同桌之间互相交流,指出图中哪些直线是具有平行关系的。
(说明:创设丰富的问题情景,体验所学知识与现实世界的联系。体现平行线的模型作用。)
这些直线平行都是给我们一种直观的感觉,那么满足什么条件的两条直线就互相平行呢?(引出课题:探索直线平行的条件)
4. 如图:D是AB上一点,过D作DE∥BC.(可用量角器)
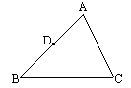
3. 已知:如图:CD平分∠ACB,∠1=∠2
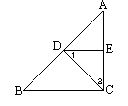
求证:DE∥BC
画图题
2. 已知:AB,CD相交于O,∠A=∠COA,∠B=∠BOD,求证:AC∥BD.
18.计算: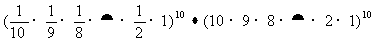 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com