2.培养学生合作交流，自主探索的良好习惯。

1.在学生了解二元一次方程组的“消元”思想，从而初步理解化“未知”为“已知”和化复杂问题为简单问题的化归思想中，享受学习数学的乐趣，增强学习数学的信息。

2.通过对具体实际问题分解,组织学生自主交流、探索,去发现列方程建模的过程,培养学生用数学的意识.

1.通过探索二元一次方程组的解法的过程,了解二元一次方程组的“消元”思想,培养学生良好的探索习惯.

5.将解方程组的技能训练与实际问题的解决融为一体,进一步提高解方程组的技能.

4.在列方程组的建模过程中,强化方程的模型思想,培养学生列方程解决实际问题的意识和能力.

3.会用二元一次方程组解决实际问题.

2.了解解二元一次方程组时的“消元思想”,“化未知为已知”的化归思想.

1.用代入法、加减法解二元一次方程组.毛

3．通过研究解决问题的方法，培养学生合作交流意识与探究精神.

重点：

用代入消元法解二元一次方程组.

难点：

探索如何用代入法将“二元”转化为“一元”的消元过程.

教学过程：

复习提问：

篮球联赛中，每场比赛都要分出胜负，每队胜一场得2分.负一场得1分，某队为了争取较好的名次，想在全部20场比赛中得到38分，那么这个队胜负场数分别是多少？

解：设这个队胜x场，根据题意得

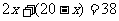
　　 解得　

　　　x＝18

　　则　20－x＝2

答：这个队胜18场，负2场.

新课：

在上述问题中，我们可以设出两个未知数，列出二元一次方程组，

　　设胜的场数是x，负的场数是y，

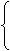　　　　x+y＝20

　　　　2x+y＝38

那么怎样求解二元一次方程组呢？上面的二元一次方程组和一元一次方程有什么关系？可以发现，二元一次方程组中第1个方程x+y＝20说明y＝20－x，将第2个方程

2x+y＝38的y换为20－x，这个方程就化为一元一次方程.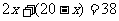

二元一次方程组中有两个未知数，如果消去其中一个未知数，将二元一次方程组转化为我们熟悉的一元一次方程，我们就可以先解出一个未知数，然后再设法求另一未知数.这种将未知数的个数由多化少、逐一解决的想法，叫做消元思想.

归纳：

上面的解法，是由二元一次方程组中一个方程，将一个未知数用含另一未知数的式子表示出来，再代入另一方程，实现消元，进而求得这个二元一次方程组的解.这种方法叫做代入消元法，简称代入法.

例1　把下列方程写成用含x的式子表示y的形式：

(1)2x－y＝3　　(2)3x+y－1＝0

例2　用代入法解方程组

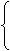　　　　　x－y＝3　　　①

　　　　3x－8y＝14　　②

例3　根据市场调查，某种消毒液的大瓶装(500g)和小瓶装(250g)两种产品的销售数量比(按瓶计算)为2:5.某厂每天生产这种消毒液22.5吨，这些消毒液应该分装大、小瓶装两种产品各多少瓶？

用代入消元法解二元一次方程组的步骤：

(1)从方程组中选取一个系数比较简单的方程，把其中的某一个未知数用含另一个未知数的式子表示出来.

(2)把(1)中所得的方程代入另一个方程，消去一个未知数.

(3)解所得到的一元一次方程，求得一个未知数的值.

(4)把所求得的一个未知数的值代入(1)中求得的方程，求出另一个未知数的值，从而确定方程组的解.

课堂练习：

教科书第107页2、3、4题

作业：

教科书第111页第1题

　　第112页第2题