
(三)归纳总结,知识回顾
这节课我们经历和体验了列方程组解决实际问题的过程,体会到方程组是刻画现实世界的有效模型,从而更进一步提高了我们应用数学的意识及解方程组的技能.
作业:
1.王大伯承包了25亩土地,今年春季改种茄子和西红柿两种大棚蔬菜,用去了
44000元,其中种茄子每亩用了1700元,获纯利2400元,种西红柿每亩用了1800元,获纯利2600元,问王大伯一共获纯利多少元?
2.一旅游者从下午2时步行到晚上7时,他先走平路,然后登山,到山顶后又沿原路下山回到出发点,已知他走平路时每小时走4千米,爬山时每小时走3千米,下坡时每小时走6千米,问旅游者一共走了多少路?
(二)导入知识,解释疑难
1.例题讲解(见P109)
分析:如果1台大收割机和1台小收割机每小时各收割小麦x公顷和y公顷,那么2台大收割机和5台小收割机1小时收割小麦______公顷,3台大收割机和2台小收割机1小时收割小麦_______公顷.
解:设1台大收割机和1台小收割机1小时各收割小麦x公顷和y公顷.根据两种工作方式中的相等关系,得方程组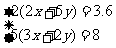
|

②-①,得11x=4.4
解这个方程,得x=0.4
把x=0.4代入①,得y=0.2
这个方程组的解是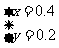
答:1台大收割机和1台小收割机1小时各收割小麦0.4公顷和0.2公顷.
2.上面解方程组的过程可以用下面的框图表示:
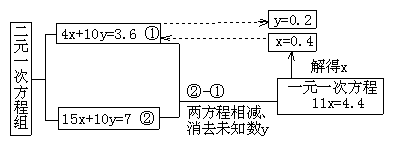
3.做一做
为了保护环境,某校环保小组成员收集废电池,第一天收集1号电池4节,5号电池5节,总重量为460克,第二天收集1号电池2节,5号电池3节,总重量为240克,试问1号电池和5号电池每节分别重多少克?
分析:如果1号电池和5号电池每节分别重x克,y克,则4克1号电池和5节5号电池总重量为4x+5y克,2节1号电池和3节5号电池总重量为2x+3y克.
解:设1号电池每节重x克,5号电池每节重y克,根据题意可得
|
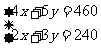
②×2-①,得y=20
把y=20代入②,得2x+3×20=240,x=90
所以这个方程组的解为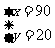
答:1号电池每节重90克,5号电池每节重20克.
4.练一练:P111练习第2、3题.
(一)指出问题,引发讨论
你能不能用二元一次方程组,帮助体育委员把表格中的两个数字补上呢?
(经过学生思考、讨论、交流)
七年级(3)班在上体育课时,进行投篮比赛,体育老师做好记录,并统计了在规定时间内投进n个球的人数分布情况,体育委员在看统计表时,不慎将墨水沾到表格上(如下表).
|
进球数n |
0 |
1 |
2 |
3 |
4 |
5 |
|
投进球的人数 |
1 |
2 |
7 |
● |
● |
2 |
同时,已知进球3个和3个以上的人平均每人投进3.5个球;进球4个和4个以下的人平均每人投进2.5个球,你能把表格中投进3个球和投进4个球对应的人数补上吗?
(三)归纳总结,知识回顾
本节课,我们主要是学习了二元一次方程组的另一解法──加减法.通过把方程组中的两个方程进行相加或相减,消去一个未知数,化“二元”为“一元”.
作业:
1.用加减法解下面方程组时,你认为先消去哪个未知数较简单,填写消元的方法.
|
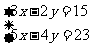 ,消元方法_________.
,消元方法_________.
|
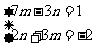 ,消元方法_________.
,消元方法_________.
2.用加减法解下列方程组:
(1) 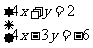 (2)
(2) 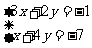
(3) 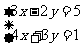 (4)
(4)
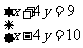
(二)导入知识,解释疑难
1.问题的解决
上面的两个方程中未知数y的系数相同,②-①可消去未知数y,得(2x+y)-(x+y)=40-22 即x=18,把x=18代入①得y=4。另外,由①-②也能消去未知数y,得(x+y)-(2x+y)=22-40 即-x=-18,x=18,把x=18代入①得y=4.
|
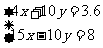
分析:这两个方程中未知数y的系数互为相反数,因此由①+②可消去未知数y,从而求出未知数x的值。
解:由①+②得 19x=11.6 x=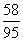
把x=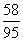 代入①得y=-
代入①得y=-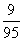 ∴这个方程组的解为
∴这个方程组的解为
3.加减消元法的概念
从上面两个方程组的解法可以发现,把两个二元一次方程的两边分别进行相加减,就可以消去一个未知数,得到一个一元一次方程。
两个二元一次方程中同一未知数的系数相反或相等时,将两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法,简称加减法。
4.例题讲解
|
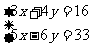
分析:这两个方程中没有同一个未知数的系数相反或相同,直接加减两个方程不能消元,试一试,能否对方程变形,使得两个方程中某个未知数的系数相反或相同。
解:①×3,得 9x+12y=48 ③
②×2,得 10x-12y=66 ④
③+④,得 19x=114
x=6
把x=6代入①,得3×6+4y=16
4y=-2, y=-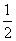
所以,这个方程组的解是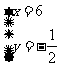
议一议:本题如果用加减法消去x应如何解?解得结果与上面一样吗?
解:①×5,得 15x+20y=80 ③
②×3,得 15x-18=99 ④
③-④,得 38y=-19
y=-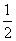
把y=-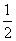 代入①,得3x+4×(-
代入①,得3x+4×(-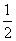 )=16
)=16
3x=18
x=6
所以,这个方程组的解为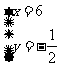
如果求出y=-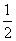 后,把y=
后,把y=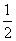 代入②也可以求出未知数x的值。
代入②也可以求出未知数x的值。
5.做一做
|
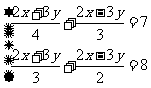
分析:本题不能直接运用加减法求解,要进行化简整理后再求解。
|
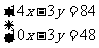
③-④,得4x=36
x=9
把x=9代入④(也可代入③,但不佳),得
10×9-3y=48
-3y=-42
y=14
∴这个方程组的解为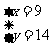
点评:当方程组比较复杂时,应先化简,并整理成标准形式.本题还可以把2x+3y和2x-3y当成两个整体,用换元法,设2x+3y=A,2x-3y=B,转化为以A、B为未知数的二元一次方程组.
6.想一想
(1)加减消元法解二元一次方程组的基本思想是什么?
(2)用加减消元法解二元一次方程组的主要步骤有哪些?
师生共析:
(1)用加减消元法解二元一次方程组的基本思路仍然是“消元”.
(2)用加减法解二元一次方程组的一般步骤:
第一步:在所解的方程组中的两个方程,如果某个未知数的系数互为相反数,可以把这两个方程的两边分别相加,消去这个未知数;如果未知数的系数相等,可以直接把两个方程的两边相减,消去这个未知数.
第二步:如果方程组中不存在某个未知数的系数绝对值相等,那么应选出一组系数(选最小公倍数较小的一组系数),求出它们的最小公倍数(如果一个系数是另一个系数的整数倍,该系数即为最小公倍数),然后将原方程组变形,使新方程组的这组系数的绝对值相等(都等于原系数的最小公倍数),再加减消元.
第三步:对于较复杂的二元一次方程组,应先化简(去分母,去括号,合并同类项等),通常要把每个方程整理成含未知数的项在方程的左边,常数项在方程的右边的形式,再作如上加减消元的考虑.
(一)提高问题,引发讨论
|
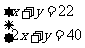 , 可以用代入消元法求解。
, 可以用代入消元法求解。
这个方程组的两个方程中,y的系数有什么关系?利用这种关系你能发现新的消元方法吗?
甲、乙、丙三位同学是好朋友,平时互相帮助。甲借给乙10元钱,乙借给丙8元钱,丙又给甲12元钱,如果允许转帐,最后甲、乙、丙三同学最终谁欠谁的钱,欠多少?
4.在用方程组解决实际问题的过程中,体验数学的实用性,提高学习数学的兴趣。
新授课:
3.体会方程组是刻画现实世界的有效数学模型,培养应用数学的意识。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com