
2. 初步体会解二元一次方程组的基本思想――“消元”.
重点
会用代入法解二元一次方程组.
活动1 消元思想与代入消元法
篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分,某队为了争取较好的名次,想在全部22场比赛中得到40分,那么这个队胜负场数分别是多少?
|
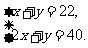
如果只设一个未知数(设胜场x场),这个问题也可以用一元一次方程:____________________________来解.
⑴观察上面的二元一次方程组和一元一次方程有什么关系?
⑵解二元一次方程组的基本思想是什么?
⑶通过小组讨论、合作与交流,你知道代入消元法的具体步骤吗?
⑷你认为代入法解二元一次方程组的过程中需要注意的是什么?
|
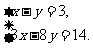
第一步:选一个系数比较简单的方程,用一个未知数表示另一个未知数
第二步:将变形后的关系式代入另一方程,消去一个未知数,得到一个一元一次方程
第三步:解这个一元一次方程,得一个未知数的值
第四步:将求得的未知数的值代入变形后的关系式,求出另一未知数的值
第五步:把求得的两个未知数的值,用“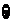 ”联立起来,就是方程组的解.
”联立起来,就是方程组的解.
活动2 简单应用
1. 会用代入法解二元一次方程组.
8.2消元----二元一次方程组的解法⑴ 学案
学习目标
3.例题教学
同约分一样,分式的通分也是对分式进行恒等变形,它的依据是分式的基本性质.通分时应注意两点:首先,通分必须依据分式的基本性质进行,不能改变原分式的值;其次,通常公分母应是最简的,否则会增大计算量,带来一些不必要的麻烦.
通分的难点是确定各分式的最简公分母,课本以分析的方式化解难点,帮助学生弄清最简公分母的构成和最简公分母的确定过程,教学时应给予足够的重视.
通分时,若分母是单项式,则取各分母系数的最小公倍数与各字母因式的最高次幂的乘积,作为公分母,这样的公分母就是最简公分母;若分母是多项式,则先将各分母分解因式,然后确定最简公分母.例3、例4分别是这两种情况的范例.
2.探索活动
(1)通过简单分数的通分,如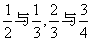 ,回顾分数通分的基本步骤;
,回顾分数通分的基本步骤;
(2)通过确定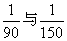 的公分母,回顾如何确定异分母分数的最小公分母;
的公分母,回顾如何确定异分母分数的最小公分母;
(3)@月§Lk66女法,确定异分母分式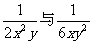 的最简公分母;
的最简公分母;
(4)通过实例,归纳分式通分的一般步骤.例如,将下列分式通分: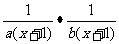
通过探索活动,建立最简公分母的概念及确定最简公分母的方法,并会将几个异分母的分式通分.
1.情境设计
设计承上启下的问题,通过问题研讨的教学活动,类比分数的通分,引导学生自主得出分式通分的概念.例如:
问题1 分式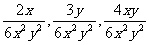 有什么共同点?试将它们分别化为最简分式.
有什么共同点?试将它们分别化为最简分式.
问题2 约分后得到的分式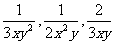 分母不相同,试将它们变形为分母相同的分式.
分母不相同,试将它们变形为分母相同的分式.
问题3 你能为“异分母分式化为同分母分式”这样的变形起一个名称,并说明为什么这样起名吗?
3.概念教学
通过联想和类比,引导学生理解分式约分的概念;
通过学生自主探索,学会如何进行分式的约分;
通过对约分的学习,引导学生理解最简分式的意义.
让学生思考:如何判断约分是否正确?分式变形的前提是不改变分式的值,因而判断变形是否正确的基本手段是,按字母的给定值检查变形前、后的分式的值是否发生了变化.
[教学过程(第三课时)]
2.探索活动
(1)结合例题教学,探索分子、分母是单项式时,如何约分?
(2)结合例题教学,探索分子、分母是多项式时,如何约分?
(3)反思:分式的约分约去了什么?约分的目的是什么?
1.情境设计
设计问题情境直接进入主题.例如:
与分数的约分类比,你能说出怎样对分式进行约分吗?你的依据是什么?
根据分数的基本性质,我们可以对分数进行约分.完成下列“尝试”,谈谈你对分式约分的理解.
4.培养学生类比推理能力.
[教学过程(第二课时)]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com