2.　　　 能根据方程组的未知数的系数特征，灵活运用代入法或加减法解方程组.

1.　　　 进一步体会消元思想，熟练地解二元一次方程组.

8. 2消元­­--二元一次方程组的解法⑸　学案

学习目标

3．通过研究解决问题的方法，培养学生合作交流意识与探究精神.

教学重点：

用代入法解二元一次方程组.

教学难点：

探索如何用代入法将“二元”转化为“一元”的消元过程.

教学过程：

复习提问：

篮球联赛中，每场比赛都要分出胜负，每队胜一场得2分.负一场得1分，某队为了争取较好的名次，想在全部22场比赛中得到40分，那么这个队胜负场数分别是多少？

解：设这个队胜x场，根据题意得

　　 解得　

　　　x＝18

　　则　22－x＝4

答：这个队胜18场，负4场.

新课：

在上述问题中，我们可以设出两个未知数，列出二元一次方程组，

　　设胜的场数是x，负的场数是y，

　　　　x+y＝22

　　　　2x+y＝40

那么怎样求解二元一次方程组呢？上面的二元一次方程组和一元一次方程有什么关系？可以发现，二元一次方程组中第1个方程x+y＝22说明y＝22－x，将第2个方程

2x+y＝40的y换为22－x，这个方程就化为一元一次方程.

二元一次方程组中有两个未知数，如果消去其中一个未知数，将二元一次方程组转化为我们熟悉的一元一次方程，我们就可以先解出一个未知数，然后再设法求另一未知数.这种将未知数的个数由多化少、逐一解决的想法，叫做消元思想.

归纳：

上面的解法，是由二元一次方程组中一个方程，将一个未知数用含另一未知数的式子表示出来，再代入另一方程，实现消元，进而求得这个二元一次方程组的解.这种方法叫做代入消元法，简称代入法.

例1　把下列方程写成用含x的式子表示y的形式：

(1)3x－y＝5　　(2)3x+2y－1＝0

例2　用代入法解方程组

　　　　　x－y＝3　　　①

　　　　3x－8y＝14　　②

例3　根据市场调查，某种消毒液的大瓶装(500g)和小瓶装(250g)两种产品的销售数量比(按瓶计算)为2:5.某厂每天生产这种消毒液22.5吨，这些消毒液应该分装大、小瓶装两种产品各多少瓶？

归纳：用代入消元法解二元一次方程组的步骤：

(1)从方程组中选取一个系数比较简单的方程，把其中的某一个未知数用含另一个未知数的式子表示出来.

(2)把(1)中所得的方程代入另一个方程，消去一个未知数.

(3)解所得到的一元一次方程，求得一个未知数的值.

(4)把所求得的一个未知数的值代入(1)中求得的方程，求出另一个未知数的值，从而确定方程组的解.

课堂练习：

P98--99页练习1、2、3、4题

作业：

P103页第1、2、4题

2．初步体会解二元一次方程组的基本思想――“消元”.

1．会用代入法解二元一次方程组.

8.2消元--二元一次方程组的解法

第一课时

教学要求：

2.　　　 某班去看演出，甲种票每张24元，乙种票每张18元.如果35名同学购票恰好用去750元，甲乙两种票各买了多少张？

拓展延伸

　甲、乙两人同解方程组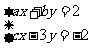，甲正确解得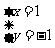，乙因抄错c，解得，求a、b、c的值.

1.　　　 用代入法解下列方程组：

⑴　　　　　　⑵

2.　　　 张翔从学校出发骑自行车去县城，中途因道路施工步行一段路，1.5小时后到达县城.他骑自行车的不尊敬速度是15千米/时，步行的平均速度是5千米/时，路程全长20千米.他骑车与步行各用多少时间？

活动3　课堂小结

这节课你学到了什么？

活动4　课堂练习