知识探索的设计是从学生熟悉的有理数运算和同底数幂的除法开始，让学生自己探索，自己感受得出新的知识.整的思路是从特殊到一般.充分调动学生去动手动脑，让学生自主探索自己总结.该学生解决的就让学生解决，教师不要代替.充分调动学生的积极性，让学生积极参加讨论，把课堂真真实实的交给学生.

(五)课堂练习：

课本第49页：练一练

(四)小结：

　 1、同底数幂除法法则中的指数还有限制吗？

　 2、本课有哪些容易混淆，出错的地方.

说明：小结时，可先让学生回答，教师补充、归纳.

(三)例题讨论：

例1：计算

(1)9²÷9²=　　　　 (2)(ab)ⁿ÷(ab)ⁿ=　　　 (3)(-3)^m÷(-3)^m =

说明：此例题旨在复习学生对同底数幂的除法性质的认识，强调了不等于0的数的0次幂等于1.

解：(略)

例2： (1)(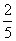)^-2　　　　 　(2)(－8)²÷(－8)⁵；　

(3)x³÷x⁸；　　 　　(4)－a³÷a⁶；　　

(5)a^3m÷a^2m－1(m是正整数)

说明：此例题旨在复习学生对同底数幂的除法性质的认识，强调了不等于0的数的负指数次幂等于这个数的幂的倒数，同时强调了幂的符号判定.

解：(略)

思考：1、当底数是分数时该如何处理？

　　　 2、运算的结果与指数中的符号有关吗？

　　　 3、指数中的符号有啥作用？

(二)知识探索：

(1)根据有理数除法法则：

2⁵÷2³=1　　　 10²÷10²=1　　　 3⁵÷3⁵=1　 　　a³÷a³=1

如果试用同底数幂除法的运算性质，可得　 2⁵÷2³=2⁰　　　 10²÷10²=10⁰　　 3⁵÷3⁵=3⁰　　　 a³÷a³=a⁰

说明：练习题的设计旨在让学生通过熟悉的知识发现问题，通过观察用两种不同方法得到的结果：2⁰ =1　 10⁰ =1　 3⁰ =1　 a⁰=1.小组讨论，小组合作，发现规律，大胆猜想总结规律，得出结论：

a⁰=1(a≠0)

任何不等于零的数的0次幂等于1.

(2)根据有理数除法法则：

2³÷2³= 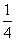　　10²÷10⁵= 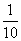　　3÷3³= 　

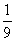
如果试用同底数幂除法的运算性质，可得2³÷2³= 2^-2　　 10²÷10⁵= 10^-1 　

3÷3³= 3^-2

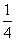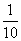说明：练习题的设计旨在让学生通过熟悉的知识发现问题，通过两种不同的方法得到两种结果，可以知道=2^-2　 　=10^-1 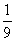　　= 3^-2；学生观察等式的特点，小组合作，小组讨论发现规律，总结规律，得出结论：

任何不等于0的数的-n(n是正整数)次幂，等于这个数的n次幂的倒数.

(一)设置情境：

情景1你能说出(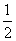－)³÷(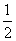－)³的结果吗？

说明：学生讨论、交流后回答，注意学生可能采取的不同的策略.对学生思维中出现的创造性火花予以鼓励，本设计旨在让学生体会同底数幂的除法和有理数的运算结果.

思考：

1、在解题过程中你用了什么知识？

2、你所得到的结果是多少？

情景2

做一做　 81=3^{(　 )} 10000=10⁴

 27=3^{(　 )} 1000=10^{(　 )}

 9=3^{(　 )} 100=10^{(　 )}

3=3^{(　 )} 　　10=10^{(　 )}

猜一猜 　1=3^{(　 )}　　　　　　　　 1=10^{(　 )}

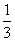　　　 　=3^{(　 )}　　　　　　　 0.1=10^{(　 )}

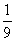　　　 　=3^{(　 )}　　　　　　 0.001=10^{(　 )}

　　　　　　　　　　　　　 0.0001=10^{(　 )}

　 说明：从以上的“做一做”和“猜一猜”使学生感受零指数幂和负指数幂的实际意义以及这种规定的合理性.

思考：

1、“做一做”中你是如何处理的？

2、“猜一猜”中你是如何想的？

有条件的用实物投影仪或多媒体演示

2、有理数零指数与负指数幂的性质的应用.

1、运用知识解决综合问题；

2、探索有理数的负指数幂的性质.