
1.有一个两位数,它的十位上的数与个位上的数的和是6,则符合条件的两位数有( )
A.4个 B.5个 C.6个 D.无数个
4.某人只带2元和5元两种货币,他要买一件27元的商品;而商店不给他找钱,要他恰好付27元,他有 种付款方式.
*慧眼识金
3.甲、乙两个团体共100人去风景区旅游风景区规定超过60人可购买团体票,已知每张团体票比个人票优惠20%,而甲、乙两团体人数均不足60人;两团体决定合起来买团体票,共优惠1600元.则团体票为每张 元.
2.某车间有62个工人,生产甲、乙两种零件,每3个甲种零件和2个一种零件配成一套.已知每人每天能加工甲种零件12个或乙种零件23个;现将62个工人分成2组,其中x人加工甲种零件,y人加工乙种零件,要使每天生产的零件配成套,则x= ,y= .
1.小明对小飞说:“我想了两个数,如果第一个数加上第二个数的一半得90;若果第二个数减去第一个数的三分之一得68.”小飞很快说出了小明想好的数.小明想好的两个数是 .
8.3再探实际问题与二元一次方程组
☆趣味导读
许多实际问题都可以通过设两个(或更多)未知数,列出方程或方程组来解决,这种方法要比其他方法简单、容易得多.下面这则小故事最早出现于《希腊文选》,读完后,试试看,聪明的你能否知道驴和骡各驮着几个包裹呢?(假定每个包裹重量相等)
驴和骡肩并肩走在街上,各自都驮着几个包裹,驴抱怨主人给它压的担子太重,骡却说:“老兄,别抱怨,你的负担并不算重!你瞧,假如你从背上拿一个包裹给我,我的负担就是你的两倍;而假如你从你的背上取走一个包裹,你的负担也不过和我相同呀!”
☆智能点拨
[例1]现有190张铁皮做盒子,每张铁皮做8个盒身或22个盒底,一个盒身与盒底配成一个完整盒子,问用多少张铁皮制盒身,多少张铁皮制盒底,可以正好制成一批完整的盒子?
[点拨]两个未知数是制盒身、盒底的铁皮张数,两个相等关系是:①制盒身铁皮张数+制盒底铁皮张数=190;②制盒身铁皮张数的2倍=制盒底铁皮张数.
[答案]设x张铁皮制盒身,y张铁皮制盒底,根据题意,得 解这个方程组,得
解这个方程组,得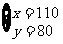 答:用110张制盒身,800张制盒底,正好制成一批完整的盒子.
答:用110张制盒身,800张制盒底,正好制成一批完整的盒子.
[例2]小明家准备装修一套新住房,若甲、乙两个装饰公司合作6周完成需工钱5.2万元;若甲公司单独做4周后,剩下的由乙公司来做,还需9周完成,需工钱4.8万元.若只选一个公司单独完成,从节约开支的角度考虑,小明家应选甲公司还是乙公司?请你说明理由.
[点拨]题目中涉及的未知数较多:甲、乙单独完成所需的时间,甲、乙单独完成所需的工钱.我们可以根据第一类等量关系:(1)甲、乙两个装饰公司合作6周完成;(2)甲公司单独做4周后,剩下的由乙公司来做,还需9周完成;列方程组求出甲、乙单独完成所需的时间.再根据另一类等量关系:(1)甲、乙两个装饰公司合作6周完成需工钱5.2万元;(2)甲公司单独做4周后剩下的由乙公司来做,还需9周完成,需工钱4.8万元,由此在得到一个方程组.
[答案]设甲公司单独完成需x周,需工钱a元;乙公司单独完成需y周,需工钱b元,依题意可得 采取换元法可解得
采取换元法可解得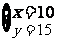 ∴依题意可得
∴依题意可得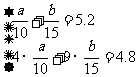 解得
解得
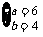 即甲公司单独完成需6万元,乙公司单独完成需4万元,故从节约的角度考虑,应选乙公司单独完成.
即甲公司单独完成需6万元,乙公司单独完成需4万元,故从节约的角度考虑,应选乙公司单独完成.
[例3]李明以两种形式分别储蓄了2000元和1000元,一年后全部取出,扣除利息所得税可得利息43.92元.已知两种储蓄年利率的和为3.24%,问这两种储蓄的年利率各是百分之几?(注:公民应缴利息所得税=利息金额×20%)
[点拨]扣税的情况:本金×年利率×(1-20%)×年数=利息(其中,利息所得税=利息
金额×20%).不扣税时:利息=本金×年利率×年数.
[答案]设第一种储蓄的年利率为x,第二种储蓄的年利率为y,根据题意,得
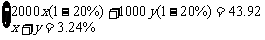 整理得
整理得 解这个方程组,得
解这个方程组,得
 答:第一种储蓄的年利率为2.25%,第二种储蓄的年利率为0.99%.
答:第一种储蓄的年利率为2.25%,第二种储蓄的年利率为0.99%.
☆随堂反馈
*画龙点睛
60(y-1)=x
解的:x=240 y=5 要使每个同学都有座位, 租用60座客车4辆,租金为:300*4=1200元;租用45座客车6辆,租金为:220*6=1320元 , 所以:租用60座客车最合算。
 15.甲种债券150元,乙种债券250元 16。设1个大瓶x元,1个中瓶y元, 1个小瓶z元,则 y=2z-0.2
15.甲种债券150元,乙种债券250元 16。设1个大瓶x元,1个中瓶y元, 1个小瓶z元,则 y=2z-0.2
x=y+z+0.4
x+y+z=9.6
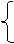 解的:x=5 y=3
z=1.6 17.解;设A点距北山X千米,则: X/4=2*(18-X)/60+X/60解X=2.25千米 18. a=50 b=100 19. 8立方米以内1.3元/立方米,超过部分2.9元/立方米. 20. 方案二获利最多. 方案一获利:2000*4*1+500*(9-4)=10500元 方案二获利: 设制成酸奶x吨,制成奶片y吨,则 x+y=9
解的:x=5 y=3
z=1.6 17.解;设A点距北山X千米,则: X/4=2*(18-X)/60+X/60解X=2.25千米 18. a=50 b=100 19. 8立方米以内1.3元/立方米,超过部分2.9元/立方米. 20. 方案二获利最多. 方案一获利:2000*4*1+500*(9-4)=10500元 方案二获利: 设制成酸奶x吨,制成奶片y吨,则 x+y=9
x/3+y/1+4=4解的:x=7.5 y=1.5方案二获利为 1200*7.5+2000*1.5=12000元
20.某牛奶加工厂现有鲜奶9吨,若在市场上直接销售,每吨可获取利润500元,制成酸奶销售,每吨可获利润1200元,制成奶片销售,每吨可获利润2000元,该工厂的生产能力为:如制成酸奶,每天可加工3吨,制成奶片每天可加工1吨,受人员限制,两种加工方式不能同时进行,受气温条件限制,这批牛奶必须在4天内全部销售或加工完毕,为此,该加工厂设计了两种可行性方案:
方案一:尽可能多的制成奶片,其余直接销售鲜牛奶.
方案二:将一部分制成奶片,其余制成酸奶销售,并恰好4天完成.
你认为选择哪种方案获利最多,为什么..
10-7答案。
19.水资源透支令人担忧,节约用水迫在眉睫,针对居民用水浪费现象,某城市制定了每月用水标准8立方米,超标部分加价收费,某户居民连续两个月的用水和水费分别为12立方米、22元,10立方米,16.2元,试求这个城市的用水标准(说明:即8立方米以内多少元/立方米,超过部分多少元/立方米).
18.某商场以每件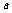 元购进一种服装,如果规定以每件
元购进一种服装,如果规定以每件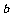 元卖出,平均每天卖出15件,30天共获利22500元,为了尽快回收资金,商场决定每件降价20%卖出,结果平均每天比降价前多卖出10件,这样30天仍可获利22500元,求
元卖出,平均每天卖出15件,30天共获利22500元,为了尽快回收资金,商场决定每件降价20%卖出,结果平均每天比降价前多卖出10件,这样30天仍可获利22500元,求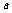 、
、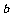 的值.(6分)
的值.(6分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com