
2.如果长方形的周长是20cm,长比宽多2cm.若设长方形的长为xcm,宽为ycm,则所列方程组为_________.
1.某哨卡运回一箱苹果,若每个战士分6个,则少6个;若每个战士分5个,则多5个,那么这个哨卡共有________名战士,箱中有_______个苹果.
3.(新疆乌鲁木齐)今年世界杯足球赛的积分方法如下:赢一场得3分,平一场得1分,输一场得0分.某小组四个队进行单循环赛后,其中一队积了7分,若该队赢了x场,平了y场,则(x,y)是( )
A.(1,4) B.(2,1) C.(0,7) D.(3,-2)
[点拨]由题意可知3x+y=7 ∵x、y都是整数,且0≤x≤3,0≤y≤3,∴只有当x=2,y=1时,符合单循环赛制,有3×2+1=7.
[答案]B.
☆单元课题研究
[提出问题]要用20张白卡纸做包装盒,每张白卡纸可以做盒身2个,或者做盒盖3个。如果1个盒身和两个底盖可以做成1个包装盒,那么能否把这些白卡纸分成两部分,一部分做盒身,一部分做盒底盖,使做成的盒身和盒底盖正好配套?请你设计一种分法.
如果不允许剪开白卡纸(即一张白卡纸不能既做盒身,又做盒底盖),能不能找到符合题意的分法?如果允许剪开一张白卡纸,怎样才能既符合题意,又能最充分的利用白卡纸?
[探究准备]解本题的关键是抓住两个等量关系:(1)做盒身的白卡纸张数+做盒底盖的白卡纸的张数=20;(2)盒底盖的个数=盒身个数的2倍.
[探究过程]设用x张白卡纸做盒身,y张白卡纸做盒底盖,根据题意,得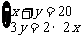 解得
解得 显然,如果不允许剪开白卡纸,就不能找到符合题意的分法.如果允许剪开白卡纸,我们可以用8张白卡纸做盒身,可做8×2=16(个);用11张白卡纸做盒底盖,
显然,如果不允许剪开白卡纸,就不能找到符合题意的分法.如果允许剪开白卡纸,我们可以用8张白卡纸做盒身,可做8×2=16(个);用11张白卡纸做盒底盖,
可做3×11(个);余下的1张白卡纸剪成两半,一半做盒身,一半做盒底盖,一共可以做17个包装盒,这样也充分地利用了材料.
[探究过程]现实生活中有许多问题,往往隐含着量与量之间的关系,可通过建立数学模型解决
2.(吉林省)二元一次方程组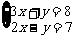 的解是 .
的解是 .
[点拨]利用加减消元法
[答案]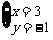
1.(2002年,湖南省)二元一次方程组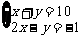 的解是( )
的解是( )
A. 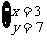 B.
B.
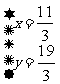 C.
C.
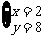 D.
D.
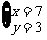
[点拨]根据二元一次方程组的解的定义知道,二元一次方程组的解必须同时使两个方程都成立.
[答案]A
3.有两个长方形,其中第一个长方形的长与宽之比为5∶4,第二个长方形的长与宽之比为3∶2,第一个长方形的周长比第二个长方形的周长大112cm,第一个长方形的宽比第二个长方形的长的2倍还大6cm,求这两个长方形的面积.
☆同步闯关
某一弹簧悬挂2kg物体时长13cm,悬挂5kg物体时长14.5cm,问:
(1)弹簧原长是多少?
(2)当悬挂3kg的物体时,该弹簧的长度是多少?
☆能力比拼
在社会实践活动中,某校甲、乙、丙三位同学一同调查了高峰时段北京二环路、三环路、四环路的车流量(每小时通过观测点的汽车量数),三位同学汇报高峰时段的车流量情况如下:
甲同学说:“二环路车流量为每小时10000辆.”
乙同学说:“四环路比三环路车流量每小时多2000辆.”
丙同学说:“三环路车流量的3倍与四环路车流量的差是二环路的2倍.”
请你根据他们所提供的信息,求出高峰时段三环路、四环路的车流量各是多少?
☆创新乐园
一位农场主,又老又病,觉得自己的日子不多了.这是他打算,按如下的次序和方式分配他的财产:
第一个儿子分100美元换剩下的财产的10%;
第二个儿子分200美元和剩下的财产的10%;
第三个儿子分300美元和剩下的财产的10%;
第四个儿子分400美元和剩下的财产的10%;
……
结果,没个儿子分的一样多,你能猜到这位老人共有几个儿子吗?


☆单元中考链接
2.甲轮船从A码头顺流而下,乙轮船从B码头逆流而上,两船同时出发相向而行,相遇于中点;而乙船顺流航行的速度是甲船逆流航行的速度的2倍.已知水流速度是4km/h,求两船在静水中的速度.
1.甲、乙两人的收入之比为4∶3,支出之比为8∶5,一年间两人各存了500元,求两人的年收入各是多少?
3.某次知识竞赛共出了25道题,评分标准如下:答对1题加4分,答错一题扣1分,不答记0分;已知李同学不答的题比答错的题多2个,他的总分为74分,则他答对了( )
A.18个 B.19个 C.20个 D.21个
☆课后沟通
2.商店购进某种商品的进价是每件8元,销售价是每件10元,现为了扩大销售量,将每件降低x%出售,但要求每件商品所获得的利润是降价前的90%,则x等于( )
A.10 B.4 C.2 D.1.8
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com