
3、某工厂第一车间比第二车间人数的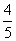 少30人,如果从第二车间调出10人到第一车间,则第一车间的人数是第二车间的
少30人,如果从第二车间调出10人到第一车间,则第一车间的人数是第二车间的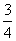 ,问这两车间原有多少人?
,问这两车间原有多少人?
解:设第一、第二车间原来分别有 x,y人
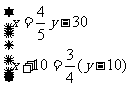
2、有大小两辆货车,两辆大车与3辆小车一次可以支货15。50吨,5辆大车与6辆小车一次可以支货35吨,求3辆大车与5辆小车一次可以运货多少吨?
解:设每辆大车和每辆小车一次运货量分别为x,y吨
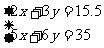
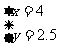

答:3辆大车与5辆小车一次可以运货24.5吨
1、某所中学现在有学生4200人,计划一年后初中在样生增加8%,高中在校生增加11%,这样全校学生将增加10%,这所学校现在的初中在校生和高中在校生人数各是多少人?
解:设现在初中在校学生有x人,高中在校生有y人
根据题意,列方程得

解这个方程组得
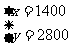
8.3 再探实际问题与二元一次方程组
教学目标:
1使学生会借助二元一次方程组解决简单的实际问题,让学生再次体会二元一次方程组与现实生活的联系和作用
2通过应用题教学使学生进一步使用代数中的方程去反映现实世界中等量关系,体会代数方法的优越性
3体会列方程组比列一元一次方程容易
4进一步培养学生化实际问题为数学问题的能力和分析问题,解决问题的能力
重点与难点:
重点:能根据题意列二元一次方程组;根据题意找出等量关系;难点:正确发找出问题中的两个等量关系
教学过程:
一复习
列方程解应用题的步骤是什么?
审题、设未知数、列方程、解方程、检验并答
新课:
看一看
课本113页探究1

问题:
1 题中有哪些已知量?哪些未知量?
2 题中等量关系有哪些?
3如何解这个应用题?
本题的等量关系是(1)30只母牛和15只小牛一天需用饲料为675kg
(2)(30+12只母牛和(15+5)只小牛一天需用饲料为940
解:设平均每只母牛和每只小牛1天各需用饲料为xkg和ykg
根据题意列方程,得
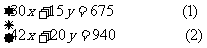
解这个方程组得
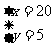
答:每只母牛和每只小牛1天各需用饲料为20kg和5kg,饲料员李大叔估计每天母牛需用饲料18-20千克,每只小牛一天需用7到8千克与计算有一定的出入。
练一练:
2、 某公园的门票价格如下表所示:
|
购票人数 |
1人-50人 |
51-100人 |
100人以上 |
|
票价 |
10元/人 |
8元/人 |
5元/人 |
某校八年级甲、乙两个班共100多人去该公园举行游园联欢活动,其中甲班有50多人,乙班不足50人。如果以班为单位分别买票,两个班一共应付920元;如果两个班联合起来作为一个团体购票,一共只要付515元。问:甲、乙两个班分别有多少人?
作业:
教材116页5、7。
1、 某山区有23名中、小学生因贫困失学要捐助。资助一名中学生的学习费用需要a元,一名小学生的学习费用需要b元。某校学生积极捐款,初中各年级学生捐款数额与用其捐助贫困中学生和小学生的部分情况如下表:
|
|
捐款数额 (元) |
捐助贫困中学生人数(名) |
捐助贫困小学生人数(名) |
|
初一年级 |
4000 |
2 |
4 |
|
初二年级 |
4200 |
3 |
3 |
|
初三年级 |
7400 |
|
|
(1) 求a、b的值。
(2) 初三学生的捐款解决了其余贫困中小学生的学习费用,请将初三年级学生可捐助的贫困中、小学生人数直接填入上表中(不必写出计算过程)。
8.3 再探实际问题与二元一次方程组(四)
命题人:赵冬玲 2005.4.25
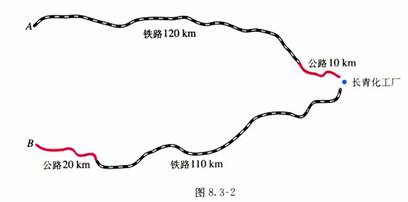 教材114页:探究3:如图,长青化工厂与A、B两地有公路、铁路相连,这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地。公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元。这批产品的销售款比原料费与运输费的和多多少元?
教材114页:探究3:如图,长青化工厂与A、B两地有公路、铁路相连,这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地。公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元。这批产品的销售款比原料费与运输费的和多多少元?
例 甲运输公司决定分别运给A市苹果10吨、B市苹果8吨,但现在仅有12吨苹果,还需从乙运输公司调运6吨,经协商,从甲运输公司运1吨苹果到A、B两市的运费分别为50元和30元,从乙运输公司运1吨苹果到A、B两市的运费分别为80元和40元,要求总运费为840元,问如何进行调运?
练习:
2. 一个安有进水管和出水管的蓄水池每单位时间内进水、出水的量是一定的,若从某时刻开始的12小时内既进水又出水,且进水时间x(小时)与蓄水池内水量
y(米3)满足关系式y=kx+b,经测得进水4小时的蓄水量为20米3,进水12小时的蓄水量为30米3。那么进水8小时的蓄水量是多少?
1.教材116页 4题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com