
1、 必做题:教科书116页习题8.3第2、6题。
养牛场原有30只母牛和15只小牛,l天约需用饲料675kg;一周后又购进12只母牛和5只小牛,这时1天约需用饲料940 kg。 饲养员李大叔估计平均每只母牛1天约需饲料18-20kg,每只小牛1天约需饲料7-8kg。你能否通过计算检验他的估计?
分析:设平均每只母牛和每只小牛1天各约需饲料xkg和ykg。
根据两种情况的饲料用量,找出相等关系,列方程组
 (1)
(1)
解这个方程组,得
 (2)
(2)
这就是说,平均每只母牛1天约需饲料_______kg,每只小牛1天约需饲料_______kg。饲养员李大叔对母牛的食量估计_______,对小牛的食量估计________。(3)
|
农作物品种 |
每公顷需劳动力 |
每公顷需投入奖金 |
|
水稻 |
4人 |
1万元 |
|
棉花 |
8人 |
1万元 |
|
蔬菜 |
5人 |
2万元 |
已知该农场计划在设备投入67万元,应该怎样安排这三种作物的种植面积,才能使所有职工都有工作,而且投入的资金正好够用?
问题:
题中有几个已知量?
题中求什么?
分别安排多少公顷种水稻、棉花、和蔬菜?
解:设安排x公顷种水稻、y公顷种棉花、则(51-x-y)种公顷蔬菜
根据题意列方程得:
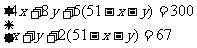
解这个方程得:
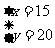
那么种蔬菜的面积为51-15-20=16
答:安排15公顷种水稻、20公顷种棉花、16种公顷蔬菜
3、 备选题:
(1)一批蔬菜要运往某批发市场,菜农准备租用汽车公司的甲、乙两种货车.已知过去两次租用这两种货车的记录如下表所示.
|
|
甲种货车(辆) |
乙种货车(辆) |
总量(吨) |
|
第1次 |
4 |
5 |
28.5 |
|
第2次 |
3 |
6 |
27 |
这批蔬菜需租用5辆甲种货车、2辆乙种货车刚好一次运完,如果每吨付20元运费,问:菜农应付运费多少元?
(2)某学校现有学生数1290人,与去年相比,男生增加20%,女生减少10%,学生总数增加7. 5%,问现在学校中男、女生各是多少?
2、 选做题:教科书117页习题8.3第9题。
1、 必做题:教科书116页习题8.3第2、6题。
8.3 再探实际问题与二元一次方程组(3)
教学目标
①进一步经历用方程组解决实际问题的过程,体会方程组是刻画现实世界的有效数学模型;
②会用列表的方式分析问题中所蕴涵的数量关系,列出二元一次方程组;
③培养分析问题、解决问题的能力,进一步体会二元一次方程组的应用价值。
教学重点与难点
重点:用列表的方式分析题目中的各个量的关系。
难点:借助列表分析问题中所蕴涵的数量关系。
教学准备
教师:课前准备例题中的图示。
教学设计
教学过程 设计意图说明
创设情境,激发兴趣
最近几年,全国各地普遍出现了夏季用电紧张的局面,为疏导电价矛盾,促进居民节约用电、合理用电,各地出台了峰谷电价试点方案。
电力行业中峰谷的含义是用山峰和山谷来形象地比喻用电负荷特性的变化幅度。一般白天的用电比较集中、用电功率比较大,而夜里人们休息时用电比较小,所以通常白天的用电称为是高峰用电,即8:00~22:00,深夜的用电是低谷用电即22:00~次日8:00。若某地的高峰电价为每千瓦时0.56元;低谷电价为每千瓦时0.28元。八月份小彬家的总用电量为125千瓦时,总电费为49元,你知道他家高峰用电量和低谷用电量各是多少千瓦时吗?
学生独立思考,容易解答。
以一道生活热点问题引入,具有现实意义。激发学生学习兴趣,同时培养学生节约、合理用电的意识。
理解题意是关键。通过该题,旨在培养学生的读题能力和收集信息能力。
探索分析,解决问题
(出示例题)如图,长青化工厂与A,B两地有公路、铁路相连。这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地。公路运价为1.5元(吨·千米),铁路运价为1.2元(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元。这批产品的销售款比原料费与运输费的和多多少元?
(图见教材115页,图8.3-2)
学生自主探索、合作交流。
设问1.如何设未知数?
销售款与产品数量有关,原料费与原料数量有关,而公路运费和铁路运费与产品数量和原料数量都有关。因此设产品重x吨,原料重y吨。
设问2.如何确定题中数量关系?
列表分析
产品x吨 原料y吨 合计
公路运费(元)
铁路运费(元)
价值(元)
由上表列方程组
解这个方程组,得
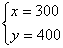
因为毛利润=销售款-原料费-运输费
所以这批产品的销售款比原料费与运输费的和多1887800元。
引导学生讨论以上列方程组解决实际问题的关键。
学生讨论、分析:合理设定未知数,找出相等关系。
本例所涉及的数据较多,数量关系较为复杂,具有一定挑战性,能激发学生探索的热情。
通过讨论让学生认识到合理设定未知数的意义。
借助表格辅助分析题中较复杂的数量关系,不失为一种好方法。
课堂练习,反馈调控
某瓜果基地生产一种特色水果,若在市场上直接销售,每吨利润为1000元;经粗加工后销售,每吨利润增为4500元;经精加工后销售,每吨利润可达7500元。一食品公司收购到这种水果140吨,准备加工后上市销售。该公司的加工能力是:每天可以精加工6吨或者粗加工16吨,但两种加工方式不能同时进行。受季节等条件限制,公司必须在15天内将这批水果全部销售或加工完毕,为此公司研制了三种可行的方案:
方案一:将这批水果全部进行粗加工;
方案二:尽可能多对水果进行精加工,没来得及加工的水果在市场上销售;
方案三:将部分水果进行精加工,其余进行粗加工,并恰好15天完成。
你认为选择哪种方案获利最多?为什么?
学生合作讨论完成。
选择经济领域问题让学生展开讨论,增强市场经济意识和决策能力,同时巩固二元一次方程组的应用。
通过对这个现实且富有挑战性的问题的讨论,培养学生勇于挑战、克服困难的意志,从中获得成功的体验。
课堂小结,知识梳理
①在用一元一次方程组解决实际问题时,你会怎样设定未知数,可借助哪些方式辅助分析问题中的相等关系?
②小组讨论,试用框图概括“用一元一次方程组分析和解决实际问题”的基本过程。
学生思考、讨论、整理。
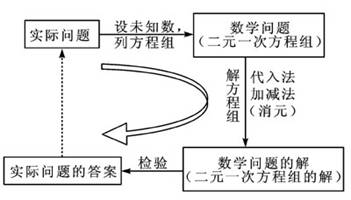
这是第一次比较完整地用框图反映实际问题与二元一次方程组的关系。
让学生结合自己的解题过程概括整理,帮助理解,培养模型化的思想和应用数学于现实生活的意识。
布置作业,自我评价
①必做题:课本第116页习题8.3第2、6题。
②选做题:课本第117页习题8.3第9题。
③备选题:
(1)一批蔬菜要运往某批发市场,菜农准备租用汽车公司的甲、乙两种货车。已知过去两次租用这两种货车的记录如下表所示。
甲种货车(辆) 乙种货车(辆) 总量(吨)
第1次 4 5 28.5
第2次 3 6 27
这批蔬菜需租用5辆甲种货车、2辆乙种货车刚好一次运完,如果每吨付20元运费,问:菜农应付运费多少元?
(2)某学校现有学生数1290人,与去年相比,男生增加20%,女生减少10%,学生总数增加7.5%,问现在学校中男、女生各是多少?
(3)为引导公民节约用水,合理利用资源,各地采用了价□教学过程□设计意图说明
格调控等手段。某地规定如下用水收费标准:每户每月的用水不超过10吨,每吨按a元收费;超过10吨,超过的部分每吨按b元收费。小颖家7、8月份的用水记录如下:
月份 用水量(吨) 水费(元)
7 12 15
8 16 21
根据以上信息,你能求出a、b的值吗?
备选题供教师参考。
本课探究的问题信息量大,数量关系复杂,未知数不容易设定,对学生来说是一种挑战,因此安排学生合作学习。学生先独立思考
|
农作物品种 |
每公顷需劳动力 |
每公顷需投入奖金 |
|
水稻 |
4人 |
1万元 |
|
棉花 |
8人 |
1万元 |
|
蔬菜 |
5人 |
2万元 |
已知该农场计划在设备投入67万元,应该怎样安排这三种作物的种植面积,才能使所有职工都有工作,而且投入的资金正好够用?
问题:
题中有几个已知量?
题中求什么?
分别安排多少公顷种水稻、棉花、和蔬菜?
解:设安排x公顷种水稻、y公顷种棉花、则(51-x-y)种公顷蔬菜
根据题意列方程得:
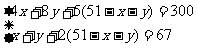
解这个方程得:
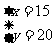
那么种蔬菜的面积为51-15-20=16
答:安排15公顷种水稻、20公顷种棉花、16种公顷蔬菜
8.3 再探实际问题与二元一次方程组(2)
教学目标
①经历用方程组解决实际问题的过程,体会方程组是刻画现实世界的有效数学模型;
②能够找出实际问题中的已知数和未知数,分析它们之间的数量关系,列出方程组;
③学会开放性地寻求设计方案,培养分析问题、解决问题的能力,体会二元一次方程组的应用价值。
教学重点与难点
重点:经历和体验用方程组解决实际问题的过程。
难点:用方程组刻画和解决实际问题的过程。
教学设计
教学过程
设计意图说明
创设情境,提出问题
前面我们初步体验了用方程组解决实际问题的全过程,其实生产、生活中还有许多问题也能用方程组解决。
(出示问题)据以往的统计资料,甲、乙两种作物的单位面积产量的比是1∶1.5,现要在一块长200m,宽100m的长方形土地上种植这两种作物,怎样把这块地分为两个长方形,使甲、乙两种作物的总产量的比是3∶4(结果取整数)?
以学生身边的实际问题展开学习,突出数学与现实的联系,培养学生用数学的意识。
探索分析,研究策略
学生自主探索,合作交流,整理思路:
(1)先确定有两种方法分割长方形;再分别求出两个小长方形的面积;最后计算分割线的位置。
(2)先求两个小长方形的面积比,再计算分割线的位置。
(3)设未知数,列方程组求解。
……
学生经讨论后发现列方程组求解较为方便。
多角度分析问题,多策略解决问题,提高思维的发散性。以上问题有哪些解法?
合作交流、解决问题
引导学生回顾列方程解决实际问题的基本思路。
(1)设未知数。
(2)找相等关系。
(3)列方程组。
(4)检验并作答。
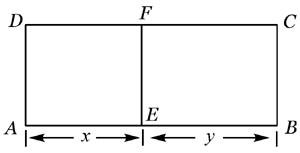
如图,一种种植方案为:甲、乙两种作物的种植区域分别为长方形AEFD和BCFE。设AE=x m,BE=y m,根据问题中涉及长度、产量的数量关系,列方程组
解这个方程组,得
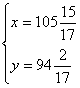 。
。
过长方形土地的长边上离一端约106m处,把这块地分为两个长方形。较大一块地种甲作物,较小一块地种乙作物。
你还能设计别的种植方案吗?
用类似的方法,可沿平行于线段AB的方向分割长方形。
教师巡视、指导,师生共同讲评。
画图,数形结合,辅助学生分析。
进一步渗透模型化的思想。
引发学生思考,寻求解决途径。
拓展探究、综合应用
学生在手工实践课中,遇到这样一个问题:要用20张白卡纸制作包装纸盒,每张白卡纸可以做盒身2个,或者做盒底盖3个,如果1个盒身和2个盒底盖可以做成一个包装纸盒,那么能否将这些白卡纸分成两部分,一部分做盒身,一部分做盒底盖,使做成的盒身和盒底盖正好配套?请你设计一种分法。
按以下步骤展开问题的讨论:
(1)学生独立思考,构建数学模型.
(2)小组讨论达成共识.
(3)学生板书讲解.
(4)对方程组的解进行探究和讨论,从而得到实际问题的结果。
(5)针对以上结论,你能再提出几个探索性问题吗?
以学生学习生活中遇到的问题展开讨论,巩固用二元一次方程组解决实际问题的一般过程,并不断提高分析问题的能力。
安排开放题,以利于培养学生探索精神和创新意识。
课堂小结、知识整理
提问:通过本节课的讨论,你对用方程解决实际的方法又有何新的认识?
生思考后回答、整理。
及时梳理总结。
布置作业
①必做题:课本第116页习题8.3第1(2)、4题。
②选做题:课本第117页习题8.3第7题。
③备选题:
①解方程组:
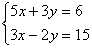
②小颖在拼图时,发现8个一样大小的矩形(如图1所示),恰好可以拼成一个大的矩形。
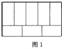
小彬看见了,说:“我来试一试。”结果小彬七拼八凑,拼成如图2那样的正方形。咳,怎么中间还留下一个洞,恰好是边长2mm的小正方形!
你能帮他们解开其中的奥秘吗?
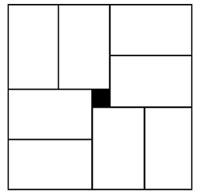
图 2
提示学生先动手实践,再分析讨论。
分层次布置作业。其中“必做题”面向全体学生,巩固知识、方法,加深理解;“选做题”面向部分学有余力的学生,给他们一定的时间和空间,相互合作,自主探究,增强实践能力。备选题供教师参考。
本课所提供的例题、练习题、作业题突出体现以下特点:
①活动性。学生在图形分割、手工操作、拼图游戏中展开数学问题的讨论,更具趣味性,学生在玩中学、做中学,在增强能力的同时,收获快乐。
②探索性。问题解决的策略不易获得,问题中的数量关系不易发现,问题中的未知数不易设定,这为学生开展探究活动提供了机会。
③开放性。解决问题的策略、方法、问题的结论的开放性设计,意在增强学生的创新意识和培养勇于挑战、克
4、某运输队送一批货物,计划20天完成,实际每天多运送5吨,结果不但提前2天完成任务并多运了10吨,求这批货物有多少吨?原计划每天运输多少吨?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com