
3.渗透类比转化的思想,让学生在学知识的同时学到方法,受到思维训练.
教学重点:
掌握分式的乘除运算
教学难点:
分子、分母为多项式的分式乘除法运算.
教学过程:
|
教学过程 |
集体讨论 |
|
|
一..情境导入: 以小丽和小明讨论 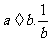 的运算顺序为情景,引人分式的混合运算--从乘,除混合运算到加,减,乘,除混合运算。 的运算顺序为情景,引人分式的混合运算--从乘,除混合运算到加,减,乘,除混合运算。二.探索活动: (1) 你怎样判断是小明的做法对,还是小丽的做法正确? (2) 你会计算 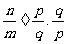 吗? 吗?(3) 怎样进行分式的乘,除混合运算?分式的加,减,乘,除混合运算吗? 三.例题教学: 例3.先化简,再求值: 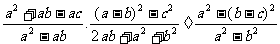 。其中 。其中 与分数混合运算类似,分式的加,减,乘,除混合运算的顺序是:先乘除,后加减。如有括号,则先进行括号内的运算。 |
|
|
|
教学过程 |
集体讨论 |
|
例4.计算:1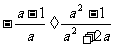 四.思维拓展: 1.已知 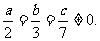 求分式 求分式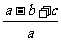 的值。 的值。2.已知 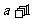 >0 >0(1)计算: 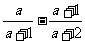 (2)比较 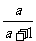 与 与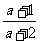 的大小 的大小3.已知: 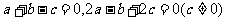 , ,求 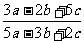 的值。 的值。 |
|
|
2.经历探索分式的乘除运算法则的过程,并能结合具体情境说明其合理性
教材62页1、2、3题平行线的
3、证平行,用判定;知平行,用性质。
2、平行线的性质与平行线的判定的区别:
 判定:角的关系 平行关系
判定:角的关系 平行关系
 性质:平行关系 角的关系
性质:平行关系 角的关系
1、说说平行线的三个性质是什么?
(四)填空:
已知:如图,∠ADE=60°,∠B=60°,∠C=80°。
问∠ AED等于多少度?为什么
 ∵ ∠ADE=∠B=60°
(已知)
∵ ∠ADE=∠B=60°
(已知)
∴ DE//BC( )
∴ ∠AED=∠C=80° ( )
(通过填空题,检验学生对平行线的判定与性质的区分)
(三)考考你:
 如图是举世闻名的三星堆考古中发掘出的一个梯形残缺玉片,工作人员从玉片上已经量得∠A=115°,∠D=100°。已知梯形的两底AD//BC,请你求出另外两个角的度数。
如图是举世闻名的三星堆考古中发掘出的一个梯形残缺玉片,工作人员从玉片上已经量得∠A=115°,∠D=100°。已知梯形的两底AD//BC,请你求出另外两个角的度数。
(学生尝试用自己的方式书写说理过程)
(二)做一做:
如图,一束平行光线AB与DE射向一个水平镜面后被反射,此时
∠1=∠2 , ∠3=∠4,
(1)∠1、∠3的大小有什么关系?∠2与∠4呢?
(2)反射光线BC与EF也平行吗?
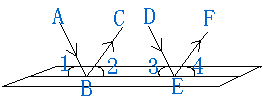
先由学生回答,用自己的语言说理,然后再出示以下说理过程,由学生说明每一步的理由。
(1) AB∥CD → ∠1=∠3 → ∠2=∠4
(2) ∠2=∠4 → BC∥EF
(一)找找看:
如图所示,AB∥CD,AC∥BD,分别找出与∠1相等或互补的角。
(学生可通过讨论交流找到所有的答案,并标注在图中)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com