
8.4 分式的乘除
[教学目标]
3.例题教学
第一课时安排了2个例题,例1是分式的乘法,例2是分式的除法,是直接运用法则进行运算的范例.应向学生说明,当分子、分母是多项式时,要先将多项式分别分解因式,变为积的形式,然后再进行运算.
由于《标准》只要求“会进行简单的分式加、减、乘、除运算”,所以课本在例1中,以分式乘法的特例形式,引人分式的乘方运算,并以卡通人的方式给出乘方运算法则,既让学生会进行乘方运算,又淡化了概念.教学时,不要把乘方运算引申、扩展到幂的运算,以避免干扰分式运算的主体.
2.探索活动
(1)你能说出这两道题的结果吗?请将你的算法告诉同学;
(2)你能验证分式乘、除运算法则是合理的、正确的吗?
与分式加、减法的探索活动(3)一样,上述探索活动(2)不一定要在每一个教学班都进行.设计此探索活动的目的是培养学生研究问题的思路与方法:对于一个猜想,首先必须合理,其次必须论证是否正确.这里,通过赋值计算,可以发现分式的乘、除运算法则不违背过去的分数运算法则,分数运算是分式运算的特例,这与分式与分数的一般与特殊的辩证关系是一致的.
(3)“约去”和“消去”的区别在哪里?
用分式(数)的分子和分母的最高公因式(最大公约数)去除分式(数)的分子和分母,把它化为最简分式(数),这叫做“约分”.在进行代数式的加减运算时,如果有两项仅系数相反,这两项可以消去.
“约去”和“消去”都是为了化简一个代数式.约去,是通过除来达到化简的目的;消去,是合并同类项以抵消,来达到化简代数式的目的.
1.情境创设
以问题征解为情境引导学生开展教学活动,探求课本中“黑板”上两题的运算方法:
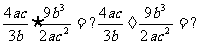
2.能正确进行分式的加、减、乘、除混合运算.
此外,通过分式乘、除运算法则的探索,感受类比的思想方法;通过对分式乘、除及混合运算法则合理性的验证,进一步培养学生“猜想需要验证”的数学素养和以理服人的良好个性品质.
[教学过程(第一课时)]
1.明确分式乘、除运算的一般步骤,能熟练地进行分式乘、除运算.
8.4 分式的乘除
[教学目标]
2、分式求值的解题步骤
1、分式混合运算的顺序
4.化简求值: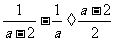 ,其中
,其中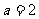 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com