
2. 难点:
针对方程组的特点,选择最好的解法.
[教学方法]
本节课采用“启发式”教学方法,通过“化归思想”引导学生进行新旧知识的迁移.
[教学流程安排]
|
活动流程图 |
活动内容目的 |
|
活动一 复习旧知 做好准备 |
通过提问复习前面所学 |
|
活动二 给出问题 列出方程 |
引入含三个未知数的方程 |
|
活动三 对比学习 明确概念 |
明确三元一次方程(组)概念 |
|
活动四 动脑动手 解方程组 |
明确指导思想选择方法 |
|
活动五 课堂练习 操作探究 |
通过练习巩固加强 |
|
活动六 归纳小结 复习所学 |
总结本节课内容,用作业巩固 |
[教学过程设计]
|
问题与情境 |
师生行为 |
设计意图 |
|
[活动1] 提问: 什么是二元一次方程? 什么是二元一次方程组? |
教师提出问题. 学生回忆作答. |
复习旧知识为学习新内容做准备. |
|
[活动2] 例:小明手头有12张面额分别为1元、2元、5元的纸币,共计22元,其中1元纸币的数量是2元纸币数量的4倍.求1元、2元、5元纸币各多少张. |
教师提出问题.学生作答. 解:设1元、2元、5元纸币分别为 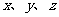 张. 张.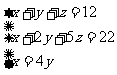 |
结合前面学习的实际问题与方程组.把实际问题转化为数学问题.引入含三个未知数的方程. |
|
[活动3] 明确概念: 含有三个未知数,并且含有未知数的项的次数都是1次的整式方程,叫做三元一次方程. 含有三种未知数,并且每个方程中含未知数的项的次数都是1次,这样的方程组叫三元一次方程组. |
教师引导学生从二元一次方程和二元一次方程组过渡到三元一次方程和三元一次方程组. 注意事项: ①区分未知数的次数与含未知数的项的次数. ②组成三元一次方程组的方程不一定都是三元一次方程. |
培养学生用旧知识学习新知识能力和类比能力.体验数学对比学习的快乐. |
|
[活动4] 解方程组: 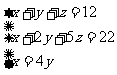 |
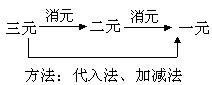 |
回忆解方程组的指导思想和操作方法.能用代入法或加减法消元.用化归思想化三元为二元,化二元为一元. |
|
[活动5] 课堂练习: 解方程组: 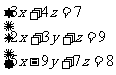 |
转化成二元一次方程组,再转化为一元一次方程.求出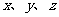 代入方程组检验,看是否解题正确. 代入方程组检验,看是否解题正确. |
培养学生动手能力,能将理论联系实际操作.感受学习的趣味. |
|
[活动6] 归纳小结: 提问学生这节课学到了什么?教师帮忙回忆总结. |
师生回忆小结本节课所学. 作业:课本第114页练习第1题、第2题. |
归纳总结本节课内容,用作业巩固. |
[设计说明]

设计意图:本课以课标理念为指导,教学设计努力体现以下几个方面:
1. 重点:
使学生会解简单的三元一次方程组,经过本课教学进一步熟悉解方程组时“消元”的基本思想和灵活运用代入法、加减法等重要方法.
3. 情感、态度与价值观
让学生通过自己的探索、尝试、比较等活动去发现一些规律,体会一些数学思想,从而激发学生的求知欲望和学习兴趣.
[重点难点]
2. 过程与方法
通过三元一次方程组的解法练习,培养学生分析能力,能根据题目的特点,确定消元方法、消元对象.培养学生的计算能力、训练解题技巧.
1. 知识与技能
(1)学习什么是三元一次方程和三元一次方程组.
(2)会解简单的三元一次方程组.
(3)掌握解三元一次方程组过程中化三元为二元和一元的化归思想.
3、这节课你有什么新的收获?
作业:
习题8、4 (2、3、4、5)
2、解题时要认真观察各个方程的系数特点,选择最好的解法.但方程组中某个方程只含二元时,一般的,这个方程缺哪个元,就利用另两个方程用加减法消哪个元;如果这个二元方程系数较简单,也可以用代入法求解.
1、解三元一次方程组的基本思想是什么?方法有哪些?
2.解二元一次方程组的基本思想是什么?
问题:小明有12张面额分别为1元、2元、5元的纸币,共计22元,其中1元纸币的数量是2元纸币数量的4倍.求1元、2元、5元纸币各多少张?
(学生思考讨论后回答下列问题)
(1)题目中有几个未知数?含有几个相等关系?你能根据题意列出几个方程?
(2)上面问题的解需要满足你列出的所有方程吗?
(3)问题(1)中的三个方程合在一起组成三元一次方程组,你能总结出三元一次方程组的含义吗?
(4) 要知道上面问题的答案,我们需要怎么做呢?
活动二 探索用“消元法”解三元一次方程组
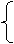 解方程组 x+y+z=12 ①
解方程组 x+y+z=12 ①
x+2y+5z=22 ②
x=4y ③
问题;(1)你能把上面的方程组化成只含有两个未知数的方程组吗?
(2)你能解出 上面 的二元一次方程组吗?
(3)如何求方程组中第三个未知数的值?
(4)总结解三元一次方程组的基本思路?
(学生通过观察方程组特点,结合上面问题独立思考后写出消元方案,然后分组交流、互相讨论后归纳出三元一次方程组的解法步骤.)
解法一:
把方程③分别代入①②,得
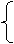 4y+y+z =12
4y+y+z =12
4y+2y+5z =22
解这个方程组, 得
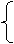 y =2,
y =2,
z=2.
把y=2,z=2代入③,得x=8.
因此, 三元一次方程组的解为
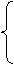 x=8,
x=8,
y=2,
z=2.
解法二:
①×5-②, 得
4x+3y=38 ④
③与④组成方程组, 得
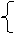 x=4y,
x=4y,
4x+3y=38.
解这个方程组, 得
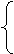 x=8,
x=8,
y=2.
把x=8,y=2代入①, 得z=2.
因此,三元一次方程组的解为
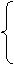 x=8,
x=8,
y=2,
z=2.
活动三 学生尝试解决例题.
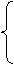 例1、解方程组 3x+4z=7 ①
例1、解方程组 3x+4z=7 ①
2x+3y+z=9 ②
5x-9y+7z=8 ③
分析: 观察方程组特点, 方程①中只含有x、z,可以由方程②③消去y, 得到一个只含x、z的方程,与方程①组成二元一次方程组.
(思考题:你还有其它解法吗?试一试,并比较那一种解法简单?)
例2、 在等式y=ax2+bx+c中,当x=-1时y=0;当x=2时y=3;x=5时y=60.求a、b、c的值.
分析: 把已知x、y的三组值分别代入y=ax2+bx+c,得到一个三元一次方程组.通过解三元一次方程组,求出a、b、c的值.
活动四 巩固练习
P114、 练习 1、2
活动五 小结,布置作业
小结:
1.解二元一次方程组的基本方法有哪几种?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com