1．情境创设

　　 问题是数学的心脏，遵循《标准》关于“方程是刻画现实世界的一种有效的数学模型”的理念，同以往一样，我们仍然从问题开始，让学生从实际问题数量关系的探索中，发现一类未知数出现在分母中的新方程--分式方程．

　　 除课本提供的3个实例外，教师可以根据学生的实际情况，补充一些与学生生活相关的实际问题，激发学生学习分式方程的兴趣．

3．会列出方程解决简单的实际问题，并能根据实际问题的意义检验所得结果是否合理．

此外，通过经历“实际问题一建立数学模型(方程)一解释、应用与拓展”的过程，体验解决问题的基本策略，发展应用意识和解决问题的技能．

[教学过程(第一课时)]

1．知道分式方程的意义，会解可化为一元一次方程的分式方程．

　　 2，了解分式方程产生增根的原因，会判断所求得的根是否是分式方程的增根．

8．5　分式方程

[教学目标]

4、市为了构建城市立体道路网络，决定修建一条轻轨铁路，为使工程提前半年完成，需将原定的工作效率提高25%.原计划完成这项工程需要多少个月？

3、改善生态环境，防止水土流失，某村计划在荒坡上种960棵树，由于青年志愿者的支援，每日比原计划多种1/3，结果提前4天完成任务，原计划每天种多少棵数？

2、小丽与小明同时为艺术节制作小红花，小明每小时比小丽多做2朵，那么小明做100朵小红花与小丽做90朵小红花所用时间相等吗？

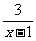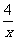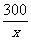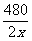1、解方程：(1)=　　　　　　　　　 (2)－=4

2、用分式方程解实际问题中的检验有哪几层含义：

1、用分式方程解实际问题的一般步骤：