1．知道分式方程的意义，会解可化为一元一次方程的分式方程．

　　 2，了解分式方程产生增根的原因，会判断所求得的根是否是分式方程的增根．

8．5　分式方程

[教学目标]

3．例题教学

通过以上探索活动，学生对解分式方程的步骤和规范表述应该有进一步的认识．例3给出了分式方程有解与无解的两种常见情况及简洁而规范的书写格式，要求学生通过练习与作业认真落实．

2．探索活动

　　 以课本上的问题“为什么所求得的根不适合原分式方程?”，引导学生探索解分式方程产生增根的现象，并讨论出现增根的原因及检验方法．例如可按以下问题串展开探索活动：

　　 (1)例1与例2的求解步骤有差异吗?

　　 (2)你能说出为什么用同样的方法求解，例1有解，而例2却无解吗?

　　 (3)你认为在解分式方程的过程中，那一步变形可能引起增根?

　　 (4)你能用较便捷的方法检验解分式方程产生的增根吗?

　　 探索时，要把握探索活动的节奏和层次：

　　 由(1)、(2)明确由于所求的根恰使原分式方程中的分母为0，从而造成原分式方程失去意义，但此分式方程解法又是正确无误的，所以断定原分式方程无解．

　　 在给出增根的定义后，再用问题(3)进一步引导学生探索产生增根的原因，感受解分式方程时验根的必要性．

　　 为使学生领悟“方程两边同乘值为0的代数式，便会产生增根”的道理，教师可以根据学生的具体情况，用浅显的例子来说明．例如，在方程x-6=0的两边同乘x，则得x(x-6)=0．若x≠0，则方程的解仍然是x=6；若x=0，则方程x(x-6)=0的解增加为两个：x=6和x=0，扩大了方程的解的范围，产生了增根．

　　 最后用问题(4)引导学生探索验根的便捷方法．

1．情境创设

　　 创设问题情境：给出分式方程无解的例题，让学生感受，既便遵循解分式方程的规范操作过程，也可能出现所求得的解并不适合原分式方程的现象，激发学生探索原委的欲望．

3．会列出方程解决简单的实际问题，并能根据实际问题的意义检验所得结果是否合理．

此外，通过经历“实际问题一建立数学模型(方程)一解释、应用与拓展”的过程，体验解决问题的基本策略，发展应用意识和解决问题的技能．

[教学过程(第二课时)]

1．知道分式方程的意义，会解可化为一元一次方程的分式方程．

　　 2，了解分式方程产生增根的原因，会判断所求得的根是否是分式方程的增根．

8．5　分式方程

[教学目标]

3．例题教学

　　 例1给出了解分式方程的一般过程及完整的书写格式，若有必要，教师可增补例题，让学生学会求解并规范表述．

2．探索活动

　　 探索活动(一)：可以采用不同的方式，探寻各个实际问题中的数量关系．例如：

对于情境(一)，可以用表格揭示服装加工中的工作总量与工作时间、个人工作效率之间的数量关系：

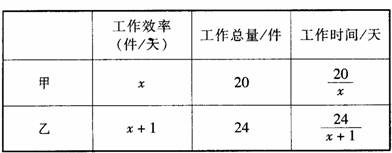
　　 根据问题中的相等关系，得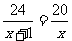

　　 对于情境(二)，可以用数位填空的方式表示两位数的构成：

　 原两位数 　　 改变后的两位数

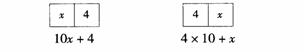
于是，可得方程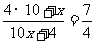

对于情境(三)，可以用线段示意图表示行程问题：

　　 由于自行车早出发40min，但与汽车同时到达，多行驶了40min，所以可得方程：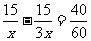

　　 探索活动(二)：探索分式方程的解法．

　　 仍以问题为先导，发动学生研究如何解分式方程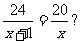

　　 学生可能会出现多种思路，例如：

　　 其一，分式方程与含有分数系数的一元一次方程“形似”，容易想到通过类比提出猜想：解分式方程也应该先去分母(卡通人语)．

　　 猜想是否正确?实践之，检验之．要强调检验的必要性，通过检验能初步说明猜想的正确性．然后告诉学生，解分式方程的一般方法是先去分母，把不熟悉的方程转化为熟悉的方程来解决．

　　 其二，移项进行减法运算，化简，得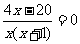

　 由分式的值为0的概念，得4x-20=0，从而得解x=5．正确否?可代人检验．

　　 其三，利用分式的基本性质，使方程两边的分式的分子为它们的最小公倍数，如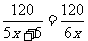，由分式相等的概念，得5x+5＝6x，从而得x=5．

　　 应注意的是，如果学生提出后两种解决问题的思路，教师则要在给予充分肯定后，引导学生继续探讨，得出解分式方程的一般方法；如果没有学生提出，则不必刻意追求，避免干扰本课主题--分式方程的一般解法．