
3. 巩固练习
(1).2x2y.3xy2
(2) .4a2x5.(-3a3bx)
课本69页--70页:第1、2题
小结与作业
2.例题
计算:(1)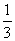 a
a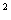 ·(6ab);
·(6ab);
(2)(2x)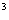 ·(-3xy
·(-3xy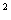 ).
).
解: (1)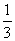 a
a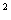 ·(6ab)
·(6ab)
= (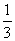 ×6)·(a
×6)·(a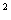 ·a)·b
·a)·b
=
2a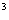 b;(教师规范格式)
b;(教师规范格式)
(2)(2x)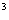 ·(-3xy
·(-3xy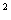 ).
).
= 8x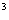 ·(-3xy
·(-3xy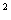 )
)
= [8×(-3)](x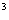 ·x)y
·x)y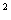
= -24x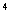 y
y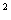 .
.
1.探索研究
一起来观察上面这个等式:3a·3b = 9ab,根据上学期的学习,同学们知道,3a、3b都是单项式,9ab也是个单项式,那么计算时是否有一定的规律性?4ab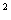 ·5b这两个单项式的积是20ab
·5b这两个单项式的积是20ab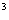 吗?
吗?
请学生回答,教师加以总结归纳:
两个单项式3a与3b相乘,只要把两个单项式的系数3与3相乘,再把这两个单项式的字母a与b相乘,即3a·3b =(3×3)·(a·b)= 9ab.
4ab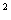 ·5b这两个单项式的积是20ab
·5b这两个单项式的积是20ab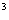 。
。
同学们回答的太棒了,两个单项式相乘,实际上是运用了乘法交换律与结合律。由此,我们可以得到单项式乘单项式法则: 单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,对于只在一个单项式里含有的字母,则连同它们的指数作为积的一个因式。
3.在活动中培养学生乐于探究、合作学习的习惯,培养学生努力寻找解决问题的进取心,体会数学的应用价值.
教学重点:分式方程的解法.
教学难点:解分式方程要验根
教学方法:引导探索法
|
教学过程 |
集体讨论内容 |
|
一、
情景创设 解方程:(1)  (2) 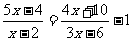 二、探索活动 1、方程(1)和方程(2)的步骤求解有差异吗? 2、你认为在解分式方程的过程中,那一步变形可能引起增根?(引导学生探索分式方程产生增根的现象,并讨论出现增根的原因让学生感受解分式方程检验根的必要性) 在这里,x=2不是原方程(2)的根,因为它使得原分式方程的分母为零,我们称它为原方程的增根.产生增根的原因是:我们在方程的两边同乘了一个可能使分母为0的整式. 因为解分式方程可能产生增根,所以解分式方程必须检验. 3、你能用比较简洁的方法检验分式方程产生的增根吗?(引导学生探索检验增根的方法) 4、想一想解分式方程一般需要经过哪几个步骤? 三、 例题教学 例1 解下列方程: (1) 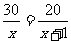 (2)
(2)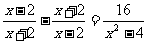 解:略 教师应该示范出简洁规范的解题过程. 注意:解分式方程时必须要验根. 解分式方程的一般步骤: 去分母(注意防止漏乘);去括号(注意先确定符号)有同类项及时的合并同类项;移项;未知数的系数化为1;验根(解分式方程必须要验根). 练习 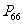 1、 ( 让学生上黑板板演) 2、 1、 ( 让学生上黑板板演) 2、四、思维拓展 解方程: 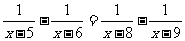 分析:若直接去分母,运算量很大且复杂,因本题的构成比较特殊,如果方程两边分别通分,则具有相同的分子,可以使解方程的过程大大的简化. 仿照此解法,你能解下面的一道题吗?试试看! 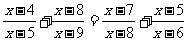 相信你能成功!思考后,你有什么收获? 五、小结 1、解分式方程的一般步骤是什么?解分式方程和我们前面学习的解一元一次方程有什么样的不同之处?又有什么样的联系? 2、谈谈你解分式方程的转化思想? 3、谈谈本节课你有什么样的收获? 六、作业布置  1、(2)(3)(4) 1、(2)(3)(4)七、板书设计 略 |
|
2.经历“求解-解释解的合理性”的过程,发展学生分析问题、解决问题的能力,培养学生的应用意识.
3. 在活动中培养学生乐于探究、合作学习的习惯,培养学生努力寻找解决问题的进取心,体会数学的应用价值.
教学重点:将实际问题中的等量关系用分式方程表示
教学难点:找实际问题中的等量关系
教学过程
|
教学过程 |
集体讨论内容 |
|
一、 情境创设 1、甲、乙两人加工同一种服装, 乙每天比甲多加工1件,已知乙加工24件服装所用时间与甲加工20件服装所用时间相同. 甲每天加工多少服装 ? 如果设甲每天加工 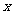 件服装,那么乙每天加工________件服装, 件服装,那么乙每天加工________件服装,根据题意,可列出方程:___________________ 2、一个两位数的各位数字是4,如果把各位数字与十位数字对调,那么所得的两位数与原两位数的比值是 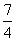 。原两位数的十位数字是几? 。原两位数的十位数字是几?如果设原两位数的十位数字是 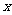 ,那么可以列出方程: ,那么可以列出方程:
3、某校学生到距离学校15km的山坡上植树,一部分学生骑自行车出发40min后,另一部分学生乘汽车出发,结果全体学生同时到达。已知汽车的速度是自行车的速度的3倍,求自行车速度。 如果设自行车的速度是 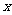 km/h,那么可列出方程: km/h,那么可列出方程:
二、探索活动 1、可以采取不同的方式,探寻各个实际问题中的数量关系。(如列表、画线段示意图等) 2、上面所得到的方程有什么共同特点?(学生可分组讨论交流) 分母中含有未知数的方程叫做分式方程。 3、分式方程与整式方程有什么区别? 4、探寻分式方程的解法:如何解分式方程 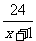 = =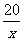 ?(让学生各抒己见) ?(让学生各抒己见)可以引导学生类比猜想,可以先猜想在验证。 说明:解分式方程的一般步骤是先去分母,;把不熟悉的分式方程转化为熟悉的一元一次方程来解决。 三、例题教学 例1 解方程: 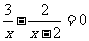 。 。教师可以板书出解分式方程的一般过程及完整的书写格式。 例2 从甲地到乙地有两条公路:一条是全长600 km的普通公路,另一条是全长480 km 的高速公路。某客车在高速公路上行驶的平均速度比在普通公路上快45 km/h,由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半。求该客车由高速公路从甲地到乙地所需的时间。 例3 (2)轮船在顺水中航行20千米与逆水航行10千米所用时间相同,水流速度为2.5千米/小时,求轮船的静水速度 练习:  1、2、3、 1、2、3、四、思维拓展 1、为了帮助遭受自然灾害的地区重建家园,某学校号召同学们自愿捐款。已知第一次捐款总额为4800元,第二次捐款总额为5000元,第二次捐款人数比第一次多20人,而且两次人均捐款额恰好相等。如果设第一次捐款人数为 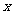 人,那么 人,那么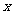 满足怎样的方程? 满足怎样的方程?2、(3)根据分式方程 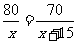 编一道应用题,然后同组交流,看谁编得好。 编一道应用题,然后同组交流,看谁编得好。五、小结 本节课你学到了哪些知识? 你有什么感想? 六、作业布置 习题8.5 1、2、 七、板书设计 |
|
2. 经历“实际问题-分式方程方程模型”的过程,发展学生分析问题、解决问题的能力,渗透数学的转化思想人体,培养学生的应用意识。
2.探索活动
采用“个人思考一小组交流一汇报方案’’的方式,尝试从不同角度寻求解决问题的方法,并能用文字、图表等手段清楚地表达解决问题的过程,并会解释结果的合理性.例如:
对于例4,有以下两种解决方案可供选择:
假设每小组有x名学生,可得分式方程: ,解得x=10,即每小组有10名学生;
,解得x=10,即每小组有10名学生;
假设原来每人平均做c面彩旗,可得分式方程: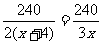 ,解得x=8,从而确定每个小组有 10名学生.
,解得x=8,从而确定每个小组有 10名学生.
例5可以仿照例4设计解决方案,但由于例5中的数量关系较例4略为复杂,所以可用表格的方式进行分析,找出数量之间的相等关系,从而得到方程.如:
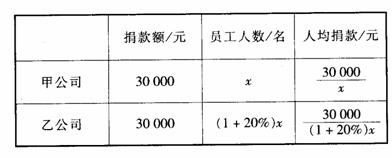
根据“乙公司比甲公司人均多捐20元”,得方程: 
通过例6的探索和求解,让学生感受在解决实际问题时,存在这样的现象:所列方程以及求得的根虽然正确,但不符合问题的实际意义,所以原实际问题仍然无解.
解分式方程(组)的检验是不可缺少的步骤.不过要注意检验的目的有两个方面:一方面是看所得数值是不是原方程的增根,另一个方面,对于应用题来讲,还要检查所得的解是否合乎实际意义
1.情境创设
课本以3个实际问题,引导学生学习用分式方程解决实际问题的基本方法,进一步感受“实际问题一建立方程一求解并解释”的过程.
有时,所列出的分式方程虽然有解,但解却不符合实际情况,这时原实际问题无解,例3的设置正是为了体现这一点.
3.会列出方程解决简单的实际问题,并能根据实际问题的意义检验所得结果是否合理.
此外,通过经历“实际问题一建立数学模型(方程)一解释、应用与拓展”的过程,体验解决问题的基本策略,发展应用意识和解决问题的技能.
[教学过程(第三课时)]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com