2．用不等式表示下列语句并写出解集：

(1)　　 x与5的差小于或等于6：

(2)　　 y与的6倍不小于12。

新课：

课堂练习：第134页 8 题，第135页 11，12，13 题。

作业：第134页 9题，第135页 10 题。

1．叙述不等式的性质。

9.1.2不等式的性质(2)

[教学目标]

掌握不等式的性质,并利用不等式的性质解决简单的实际问题。

　[教学重点与难点]

重点:不等式的性质和解法.在实际问题中建立一元一次不等式的数量关系。

难点:根据实际问题建立一元一次不等式

关键：会用不等式刻画数量关系。

[教学设计]

教学过程：

复习：

根据不等式的性质,把下列不等式化为x>a或x<a的形式

学生观察规律

归纳性质

简单应用性质

式:

(1)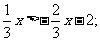(2)

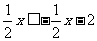
(3)-3x>2;(4)-3x+2<2x+3

例3　 　已知不等式3x-a≤0的解集是x≤2，求a的取值范围.

[作业]

必做题:教科书134页习题:6题

教案编写:莫大勇

问题1 等式的性质1,2.

问题2 用”>””<” 填空并总结规律:

　　 请　　 　

(1)5>3 ,5+2　　　 3+2,5-2　　　 3-2

(2)-1<3,-1+2　　 3+2,-1-3　　 3-3

(3)6>2,6×5　　　 2×5,6×(-5)　　　 2×(-5)

(4)-2<3,(-2)×6　　 3×6,(-2)×(-6)　　　 3×(-6)

由上面规律填空:

(1)当不等式两边加上或减去同一个数(正数或负数)时,不等号的方向　　　　　　　　　　 ;

(2)当不等式两边乘同一个正数时,不等号的方向　　　　　 ;而乘同一个负数时,不等号的方向　　　　 .

不等式性质:

(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.

(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.

(3)不等式来年改变乘(或除以)同一个负数,不等号的方向改变.

例1 利用不等式的性质，填”>”,:<”

(1)若a>b,则2a+1　　　 2b+1;

(2)若-1.25y<10,则y　　　　 -8;

(3)若a<b,且c>0,则ac+c　　　 bc+c;

(4)若a>0,b<0,c<0,则(a-b)c　　　 0.

　例2　 利用不等式性质解下列不等式

(1)x-7>26;　 (2)3x<2x+1;

(3)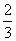x>50; (4)-4>3.

分析:利用不等式性质变形为最基本形,利用数轴表示解集

练习:教材133:1,2题..

2．用不等式表示下列语句并写出解集：

(1)　　 x与5的差小于或等于6：

(2)　　 y与的6倍不小于12。

新课：

课堂练习：第134页 8 题，第135页 11，12，13 题。

作业：第134页 9题，第135页 10 题。

1．叙述不等式的性质。

9.1.2不等式的性质(2)

[教学目标]

掌握不等式的性质,并利用不等式的性质解决简单的实际问题。

　[教学重点与难点]

重点:不等式的性质和解法.在实际问题中建立一元一次不等式的数量关系。

难点:根据实际问题建立一元一次不等式

关键：会用不等式刻画数量关系。

[教学设计]

教学过程：

复习：

根据不等式的性质,把下列不等式化为x>a或x<a的形式

学生观察规律

归纳性质

简单应用性质

式:

(1)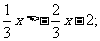(2)

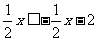
(3)-3x>2;(4)-3x+2<2x+3

例3　 　已知不等式3x-a≤0的解集是x≤2，求a的取值范围.

[作业]

必做题:教科书134页习题:6题

教案编写:莫大勇

问题1 等式的性质1,2.

问题2 用”>””<” 填空并总结规律:

　　 请　　 　

(1)5>3 ,5+2　　　 3+2,5-2　　　 3-2

(2)-1<3,-1+2　　 3+2,-1-3　　 3-3

(3)6>2,6×5　　　 2×5,6×(-5)　　　 2×(-5)

(4)-2<3,(-2)×6　　 3×6,(-2)×(-6)　　　 3×(-6)

由上面规律填空:

(1)当不等式两边加上或减去同一个数(正数或负数)时,不等号的方向　　　　　　　　　　 ;

(2)当不等式两边乘同一个正数时,不等号的方向　　　　　 ;而乘同一个负数时,不等号的方向　　　　 .

不等式性质:

(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.

(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.

(3)不等式来年改变乘(或除以)同一个负数,不等号的方向改变.

例1 利用不等式的性质，填”>”,:<”

(1)若a>b,则2a+1　　　 2b+1;

(2)若-1.25y<10,则y　　　　 -8;

(3)若a<b,且c>0,则ac+c　　　 bc+c;

(4)若a>0,b<0,c<0,则(a-b)c　　　 0.

　例2　 利用不等式性质解下列不等式

(1)x-7>26;　 (2)3x<2x+1;

(3)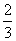x>50; (4)-4>3.

分析:利用不等式性质变形为最基本形,利用数轴表示解集

练习:教材133:1,2题..