2、已知，9a^n-3b²ⁿ与-2a^3mb^5-n的积与5a⁴b⁹是同类项，求m, n的值.

1、计算：

(1)(2aⁿ⁺²)·(-3a^n-1)　　　　　　　　　　　　　　　　　　　　　　 (2) (-1.2×10²)²×(5×10³)³×(2×10⁴)²

(3) 5x³y·(-3y)²+(-6xy)²·(-xy)+xy³·(-4x²)　　　　　　　　　 (4)(3×2)¹⁰×(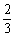×25)¹⁰ 　　　

4、如图，计算绿地(阴影部分)的面积.

[课外延伸](仔细想一想，你是最棒的)

3、计算：

(1) -3xy·2xy　　　　　　　　　　　　　　　　　　　　　　 (2) 3a²b·2ab·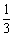abc²

(3) (-3ab)·(-a²c)·6ab²c　　　　　　　　　　　　　 (4) 2(x+y)·3(x+y)²·(x+y)⁵

(5) (2×10³)× (3×10⁴)×(-3×10⁵)　　　　　　　　　 (6) (-x)⁵·(xy)²·x³y

(7) (-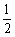m³n)³·(-2m²n)⁴　　　　　　　　　　　　　　　　　 (8) (2a²b³)³·(-3a²b)²·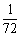abc

　(9) (-3x²y)³·xyz·(-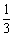xy)²　　　　　　　　　　　　　　 (10) [-2(x-y)²]²·(y-x)³

(11) aⁿb²·(aⁿ⁺¹·b⁴)²　　　　　　　　　　　　　　　　 (12) (-2sⁿ⁺¹)⁴·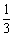sⁿ·t

2、选择：

(1)下列运算中，正确的是　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A、a¹⁰÷a⁵=a²　　　　 B、(a³)⁴=a⁷　　　　　 C、(x-y)²=x²-y²　　 　 D、4a³·(-3a³)=-12a⁶

(2)若(mx⁴)·(4x^k)=-12x¹²，则适合条件的m, k的值应是　　　　　　 (　　 )

A、m=3, k=8　　　　 B、m=-3, k=8　　　　　　　 C、m=8, k=3　　　　　　　 D、m=-3, k=3

1、下列计算是否正确？不正确的，指出错在哪里，并改正：

(1)3x⁴·2x²=6x⁶　　　　　　　　　　　　　　 　　　　　　　　 (　 　　 　　　 )

(2)ab²·3abc=3a²b³　　　　　　　　　　　 　　　　　　　　 (　　　　 　　 )

(3)4xy·(-7xy)=-28xy　　　　　　　　　 　　　　　　　　 (　　　　 　　 )

(4)6a⁸·6a⁸=12a¹⁶　　　　　　　　　　　　 　　　　　　　　 (　　　　 　　 )

9.1　 单项式乘单项式

班级　　　　　　　　　　 　 姓名　　　　　　　　　 　　　 学号　　　　　　　

[基础训练](认真填一填，相信你会行)

2．用不等式表示下列语句并写出解集：

(1)　　 x与5的差小于或等于6：

(2)　　 y与的6倍不小于12。

新课：

课堂练习：第134页 8 题，第135页 11，12，13 题。

作业：第134页 9题，第135页 10 题。

1．叙述不等式的性质。

9.1.2不等式的性质(2)

[教学目标]

掌握不等式的性质,并利用不等式的性质解决简单的实际问题。

　[教学重点与难点]

重点:不等式的性质和解法.在实际问题中建立一元一次不等式的数量关系。

难点:根据实际问题建立一元一次不等式

关键：会用不等式刻画数量关系。

[教学设计]

教学过程：

复习：