
2.如果点(a,-2a)在函数y=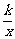 的图象上,那么k______0.(填“>”或“<”)
的图象上,那么k______0.(填“>”或“<”)
1.反比例函数y=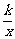 的图象经过点(-2,-1),那么k的值为_________.
的图象经过点(-2,-1),那么k的值为_________.
2、
反比例函数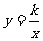 (k≠0)中自变量的范围是什么?比例系数是多少?
(k≠0)中自变量的范围是什么?比例系数是多少?
答:x≠0;k。
范例点睛
例1. 判断下列关系式中y和x是反比例函数关系吗?若是,指出比例系数.
(1)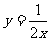 ;(2)
;(2)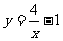 ; (3)
; (3) 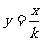 (k≠0) ; (4)
(k≠0) ; (4)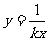 (k≠0).
(k≠0).
易错辨析:(2)和(3)都不满足反比例函数的形式,
(1)(4)是反比例函数关系式,但注意比例系数分别是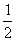 和
和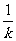 .
.
例2.已知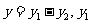 与x成正比例,
与x成正比例,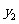 与x-2成反比例,当x=1时,y=2;当x=3时,y=1,求y与x的函数关系式.
与x-2成反比例,当x=1时,y=2;当x=3时,y=1,求y与x的函数关系式.
思路点拨:首先要表示出y 与x和y
与x和y 与x的函数表达式,注意这里的比例系数是不同的(设k
与x的函数表达式,注意这里的比例系数是不同的(设k ,k
,k );其次,再由y=y
);其次,再由y=y -y
-y ,列出y与x的关系式.然后利用两组数据求出函数的解析式.
,列出y与x的关系式.然后利用两组数据求出函数的解析式.
易错辨析:在本题中容易出现两种错误,没有区分两个比例系数,只设了一个k;或者设两个比例系数,却把x=1,y=2 代入y 的解析式,把x=3,y=1代入y
的解析式,把x=3,y=1代入y 的解析式.
的解析式.
方法点评:在解决这一类问题时,先根据题意设出解析式,然后再把已知数据代入,最后解关于字母的方程(组).
课外链接
我们学习过反比例函数,例如当工作总量a一定时,工作天数m和日工作量n之间的关系式可以写成m=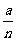 (a为常数,a≠0).
(a为常数,a≠0).
请你仿照上例另举一个在日常生活和学习中具有反比例函数关系的实例,并写出函数关系式.
实例:____________________________________________________________
___________________________________________________________________________.
函数关系式:______________________________________________________.
随堂演练
1、
判断下列关系式中y分别是x的什么函数:(1)y=-x;(2)y=2x-1;(3)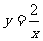 ;(4)xy=3.
;(4)xy=3.
答:(1)是正比例函数;(2)是一次函数;(3)(4)是反比例函数。
9.1反比例函数
新知导读
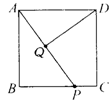
12.如图,在边长为2的正方形ABCD中,P为BC边上的任意一点(点P与B、C不重合),且DQ⊥AP,垂足为Q,设AP=x,DQ=y.
(1)如果连接DP,那么△ADP的面积等于_________;
(2)当点P为BC上的一个动点时,线段DQ也随之变化,若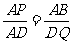 ,求y与x之间的函数关系式,并指出x的取值范围.
,求y与x之间的函数关系式,并指出x的取值范围.
11.下图中有一面围墙(可利用的最大长度为100m),现打算沿墙围成一个面积为120m2的长方形花辅.设花辅的一边AB=x(m),另一边为y(m),求y与x的函数关系式,并指出其中自变量的取值范围.

10.举出生活中变量具有反比例函数关系的实例(1-2例).
[拓展与延伸]
9.已知三角形的面积为100cm2,求三角形的边长y(cm)与该边上的高x(cm)之间的函数关系式,并写出自变量的取值范围.
8.关系式y=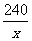 可以表示的实际意义为___________.
可以表示的实际意义为___________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com