练习册

  • 练习册
  • 试题
     0  205973  205981  205987  205991  205997  205999  206003  206009  206011  206017  206023  206027  206029  206033  206039  206041  206047  206051  206053  206057  206059  206063  206065  206067  206068  206069  206071  206072  206073  206075  206077  206081  206083  206087  206089  206093  206099  206101  206107  206111  206113  206117  206123  206129  206131  206137  206141  206143  206149  206153  206159  206167  447090 

    问题1 汽车从南京出发开往上海(全程约300km)，全程所用时间t(h)随速度v(km/h)的变化而变化.

    (1)你能用含有v的代数式表示t吗？

    (2)利用(1)的关系式完成下表

    v(km/h)
    		 60
    		 80
    		 90
    		 100
    		 120
    t(h)
    		 　
    		 　
    		 　
    		 　
    		 　

    随着速度的变化，全程所用的时间发生什么变化？

    (3)速度是时间t的函数吗？为什么？

    问题2、学校课外生物小组的同学准备自已动手,用旧围栏建一个面积为24平方米的矩形饲养场,假设它的一边长为x(米)，求另一边的长y(米)与x的函数关系式.

    答：　　　　　　　　　　　　　　　　　　　　　　　　　

    试题详情

    回顾小学所学的反比例，请举出两个反比例关系的事例.

    (1)：　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

    (2)：　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

    试题详情

    活　动　内　容
    		 师生互动思考与安排
    1、写出下列问题中两个变量之间的函数关系式，并判断其是否为反比例函数. 如果是，指出比例系数k的值.
    (1)底边为5cm的三角形的面积y(cm2)随底边上的高x(cm)的变化而变化；
    (2)某村有耕地面积200ha，人均占有耕地面积y(ha)随人口数量x(人)的变化而变化；
    (3)一个物体重120N，物体对地面的压强p(N/m2)随该物体与地面的接触面积S(m2)的变化而变化.
    2、下列哪些关系式中的y是x的反比例函数？如果是，比例系数是多少？
    (1)y＝x；　 (2)y＝；　 (3)xy+2＝0；
    (4)xy＝0；　(5)x＝.
    3、已知函数y＝(m+1)x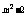是反比例函数，则m的值为　　.
    ［说明］引导学生分析、讨论，列出函数关系式，并检验是否是反比例函数，指出比例系数.
    第3题要引导学生从反比例函数的变式y＝kx－1入手，注意隐含条件k≠0，求出m值.
    　
    　
    　
    　
    　
    		 　

    试题详情

    活　动　内　容
    		 师生互动思考与安排
    例1：下列关系式中的y是x的反比例函数吗？如果是，比例系数k是多少？
    (1)y＝；(2)y＝；(3)y＝－ ；(4)y＝－3；(5)y＝；(6)y＝+2；(7)y＝.
    ［说明］这个例题作了一些变动，引导学生充分讨论，把函数关系式如何化成y＝或y＝kx+b的形式了解函数关系式的变形，知道函数关系式中比例系数的值连同前面的符号，会与一次函数的关系式进行比较，若对反比例函数的定义理解不深刻，常会认为(2)与(4)也是反比例函数，而(2)式等号右边的分母是x－1，不是x，(2)式y与x－1成反比例，它不是y与x的反比例函数. 对于(4)，等号右边不能化成 的形式，它只能转化为的形式，此时分子已不是常数，所以(4)不是反比例函数. 而(7)中右边分母为2x，看上去和(2)类似，但它可以化成，即k＝－，所以(7)是反比例函数. 通过这个例题使学生进一步认识反比例函数概念的本质，提高辨别的能力.
    例2：在函数y＝－1，y＝，y＝x－1，y＝中，y是x的反比例函数的有　个.
    ［说明］这个例题也是引导学生从反比例函数概念入手，着重从形式上进行比较，识别一些反比例函数的变式,如y＝kx－1的形式. 还有y＝－1通分为y＝，y、x都是变量，分子不是常量，故不是反比例函数，但变为y+1＝可说成(y+1)与x成反比例.
    例3：若y与x成反比例，且x＝－3时，y＝7，则y与x的函数关系式为　　　.
    ［说明］这个例题引导学生观察、讨论，并回顾以前求一次函数关系式时所用的方法，初步感知用“待定系数法”来求比例系数，并引导学生归纳求反比例函数关系式的一般方法，即只需已知一组对应值即可求比例系数.
    		 　

    试题详情

    活　动　内　容
    		 师生互动思考与安排
    情境1：
    当路程一定时，速度与时间成什么关系？(s＝vt)
    当一个长方形面积一定时，长与宽成什么关系?
    ［说明］这个情境是学生熟悉的例子，当中的关系式学生都列得出来，鼓励学生积极思考、讨论、合作、交流，最终让学生讨论出：当两个量的积是一个定值时，这两个量成反比例关系，如xy＝m(m为一个定值)，则x与y成反比例。
    这一情境为后面学习反比例函数概念作铺垫。
    情境2：
    汽车从南京出发开往上海(全程约300km)，全程所用时间t(h)随速度v(km/h)的变化而变化.
    问题：
    (1)你能用含有v的代数式表示t吗？
    (2)利用(1)的关系式完成下表：
    v/(km/h)
    		 60
    		 80
    		 90
    		 100
    		 120
    t/h
    		 　
    		 　
    		 　
    		 　
    		 　

    随着速度的变化，全程所用时间发生怎样的变化？

    (3)速度v是时间t的函数吗？为什么？

    		 　
    ［说明］(1)引导学生观察、讨论路程、速度、时间这三个量之间的关系，得出关系式s＝vt，指导学生用这个关系式的变式来完成问题(1).
    (2)引导学生观察、讨论，并运用(1)中的关系式填表，并观察变化的趋势，引导学生用语言描述.
    (3)结合函数的概念，特别强调唯一性，引导讨论问题(3).
    情境3：
    用函数关系式表示下列问题中两个变量之间的关系：
    (1)一个面积为6400m2的长方形的长a(m)随宽b(m)的变化而变化；
    (2)某银行为资助某社会福利厂，提供了20万元的无息贷款，该厂的平均年还款额y(万元)随还款年限x(年)的变化而变化；
    (3)游泳池的容积为5000m3，向池内注水，注满水所需时间t(h)随注水速度v(m3/h)的变化而变化；
    (4)实数m与n的积为－200，m随n的变化而变化.
    问题：
    (1)这些函数关系式与我们以前学习的一次函数、正比例函数关系式有什么不同？
    (2)它们有一些什么特征？
    (3)你能归纳出反比例函数的概念吗？
    一般地，形如y＝(k为常数，k≠0)的函数称为反比例函数，其中x是自变量，y是x的函数，k是比例系数.
    反比例函数的自变量x的取值范围是不等于0的一切实数.
    ［说明］这个情境先引导学生审题列出函数关系式，使之与我们以前所学的一次函数、正比例函数的关系式进行类比，找出不同点，进而发现特征为：(1)自变量x位于分母，且其次数是1.(2)常量k≠0.(3)自变量x的取值范围是x≠0的一切实数.(4)函数值y的取值范围是非零实数.并引导归纳出反比例函数的概念，紧抓概念中的关键词，使学生对知识认知有系统性、完整性，并在概念揭示后强调反比例函数也可表示为y＝kx－1(k为常数，k≠0)的形式，并结合旧知验证其正确性.
    		 　

    试题详情

    3. 能判断一个给定函数是否为反比例函数.通过探索现实生活中数量间的反比例关系，体

    会和认识反比例函数是刻画现实世界中特定数量关系的一种数学模型；进一步理解常量与变量的辩证关系和反映在函数概念中的运动变化观点.

    试题详情

    2. 能根据实际问题中的条件确定反比例函数的关系式.

    试题详情

    1. 理解反比例函数的概念，能判断两个变量之间的关系是否是函数关系，进而识别其中的反比例函数.

    试题详情

    本节课的我们从学生熟悉的事例入手，创设问题情境，让学生在经历分析问题中各种量的关系的过程中，认识生活中的反比例关系，并根据这一认识继续创设情境，运用类比的思想方法与一次函数、正比例函数比较，得出反比例函数、比例系数的概念，通过这一点让学生明白生活中处处有数学，引发学生学习反比例函数的热情，使学生在主动探索中进一步体会反比例函数是刻画现实世界的一种有效的数学模型；结合情境1中的问题，认识反比例是怎么回事，理解反比例的意义，让学生认识当两个量的积是一定值时，这两个量成反比例关系，为下面学习反比例函数打好基础，让学生在列函数关系式的探索过程中掌握知识，形成技能，并在数学活动中给学生留下充分的时间思考练习及讨论，识别反比例函数及比例系数，初步感知用“待定系数法”确定比例系数，识别y＝kx－1(k为常数，k≠0)和xy＝k(k≠0)的形式，进行简单运用，以此提高学生解决问题的应变能力、分析判断能力和创新意识.

    试题详情

    13.反比例函数y=­­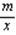与一次函数y=kx+b的图象的一个交点为A(－2,－1),并且在x=3­时,­这两个函数的值相等,求这两个函数的解析式?

    试题详情


    同步练习册答案