
4.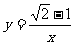 5,
5,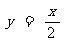 6.
6.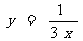
例2 若函数 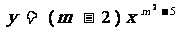 是反比例函数,求出m的值并写出解析式.
是反比例函数,求出m的值并写出解析式.
练习2 当a= 时,函数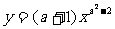 是反比例函数?
是反比例函数?
例3 若y与x成反比例,且x=-3时,y=7,则y与x的函数关系式为 .
练习3,反比例函数 (k≠0)的图象经过(1,-3),则k的值是
.
(k≠0)的图象经过(1,-3),则k的值是
.
挑战自我:
1.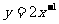 2,
2,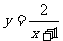 3.
3.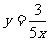
3.  4.
4.

练习1,下列关系式中y是x的反比例函数的是:
1. 2.
2. 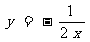
2.什么是函数关系?
|
2 情景创设: 1),汽车从南京出发开往上海(全程约300km),全程所用时间t(h)随速度v(km/h)的变化而变化. 问题: ① 你能用含有v的代数式表示t吗? ② 利用(1)的关系式完成下表: 随着速度的变化,全程所用时间发生怎样的变化?
|
60 |
80 |
90 |
100 |
120 |
|
|
t/h |
|
|
|
|
|
③ 速度v是时间t的函数吗?为什么?
2),用函数关系式表示下列问题中两个变量之间的关系:
① 一个面积是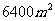 的长方形的长a(m)随宽b(m)的变化而变化
的长方形的长a(m)随宽b(m)的变化而变化
则a关于b的关系式为_____.
②,京沪线铁路全程为1463 km,某列车平均速度为 v(km/
h),全程运行时间为 t(h),则v关于t的关系式为_____
③ ,已知三角形的面积S是常数,它的底边长y与底边上的高x之间的关系式为_____
④,实数m与n的积是-200,m关于n的关系式为_____
3 交流:
(1)这些函数关系式与我们以前学习的正比例函数关系式有什么不同?
(2)它们有一些共同什么特征?
(3)你能归纳出反比例函数的概念吗?
4,反比例函数的定义:
反比例函数自变量取值范围:
5,例题与练习:
例1,下列关系式中y是x的反比例函数吗?如果是,k的值是多少?
3. 会求简单实际问题中反比例函数解析式.
教学重点:理解和领会反比例函数的概念.
教学难点:对反比例函数定义的应用.
教学过程:
1 知识回顾:1.什么是反比例关系?
2. 能根据实际问题中的条件确定反比例函数的关系式.
1.理解反比例函数的概念,能判断两个变量之间的关系是否是函数关系,进而识别其中的反比例函数.
9.1 反比例函数
教学目标:
8.已知一个长方体的体积是100立方厘米,它的长是ycm,宽是5cm,高是xcm.
(1)写出用高表示长的函数式;
(2)写出自变量x的取值范围;
(3)当x=3cm时,求y的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com