
1、若y与x成反比例,且x=-3时,y=7,则y与x的函数关系式是 .
4、 布置作业:
课本79页 习题9.1 1、2
补充:
3、 小结与思考
小结(略)
思考:
反比例函数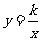 (k为常数,k≠0)的自变量x的取值范围为不等于0的实数.但在实际问题中,反比例函数的自变量取值范围往往受到限制,比如:
(k为常数,k≠0)的自变量x的取值范围为不等于0的实数.但在实际问题中,反比例函数的自变量取值范围往往受到限制,比如:
(1)一名工人加工80个零件的时间y(h)随该工人每小时能加工零件个数x(个/小时)的变化而变化,函数关系式为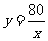 .求该函数的自变量范围.
.求该函数的自变量范围.
(2)一个面积为6400㎡的长方形的长a(m)随宽b(m)的变化而变化,函数关系式为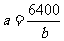 .求该函数的自变量的范围.(长是大于宽的)
.求该函数的自变量的范围.(长是大于宽的)
2、 探索活动:
活动一:
汽车从南京出发开往上海(全程约为300km),全程所用的时间t(h)随速度v(km/h)的变化而变化.
(1)你能用含有v的代数式表示t吗? 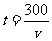
(2)利用(1)中的关系式完成下表:
|
v/(km/h) |
60 |
80 |
90 |
100 |
120 |
|
t/h |
|
|
|
|
|
随着速度的变化,全程所用的时间发生怎样的变化?
速度变大,时间减小;速度变小,时间增大.
(3)速度v是时间t的函数吗?为什么?
活动二:
(1)利函数关系式表示下列问题中的两个变量之间的关系:
①一个面积为6400㎡的长方形的长a(m)随宽b(m)的变化而变化;
函数关系式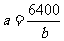
②某银行为资助某社会福利厂,提供了20万元的无息贷款,该厂的平均年还款额y(万元)随还款年限x(年)的变化而变化;
函数关系式
③实数m与n的积为-200,m 随n的变化而变化;
函数关系式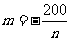
④一名工人加工80个零件的时间y(h)随该工人每小时能加工零件个数x(个/小时)的变化而变化.
函数关系式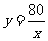
(2)交流:
函数关系式: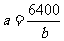 、
、 、
、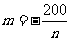 、
、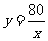 具有什么共同特征?
具有什么共同特征?
定义: 一般地,形如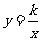 (k为常数,k≠0)的函数称为反比例函数,其中x是自变量,y是函数,k是比例系数.
(k为常数,k≠0)的函数称为反比例函数,其中x是自变量,y是函数,k是比例系数.
①反比例函数的自变量x的取值范围是不等于0的一切实数.
②反比例函数的函数值y的取值范围是不等于0的一切实数.
③指出上述4个反比例函数的比例系数.
例1、下列关系中的y是x的反比例函数吗?如果是,比例系数k是多少?
(1)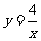 ;(2)
;(2)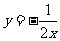 ;(3)
;(3)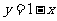 ;(4)
;(4)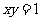 ;(5)
;(5)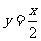
(6)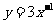 ;(7)
;(7)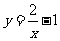
练习:课本78页
注: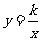 (k为常数,k≠0)可以写成
(k为常数,k≠0)可以写成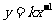 (k为常数,k≠0).
(k为常数,k≠0).
例2、 已知函数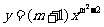 是反比例函数,求m的值.
是反比例函数,求m的值.
练习:已知函数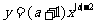 是反比例函数,求a的值.
是反比例函数,求a的值.
(4) 思考:
①你还能举出反比例函数的实例吗?
练习:课本78页 1
② 对于反比例函数 ,它还能表示什么其它的实际意义?
,它还能表示什么其它的实际意义?
1、 情境创设:
在速度v,时间t与路程s之间满足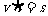 :
:
(1) 如果速度v一定时,路程s随时间t的增大而增大,路程s与时间t就成正比例关系.且对于时间t的每一个值,路程s都有唯一的一个值与它对应,它又是函数关系.因此,如果速度v一定时,路程s是时间t的正比例函数.
(2) 如果时间t一定时,那么路程s与速度v又是什么关系呢?
(3) 如果路程s一定时,那么速度v和时间t又是什么关系呢?[反比例关系:如果两个量x、y满足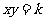 (k为常数,k≠0),那么x、y就成反比例关系.],是函数关系吗?
(k为常数,k≠0),那么x、y就成反比例关系.],是函数关系吗?
2、感受反比例函数是刻画世界数量关系的一种有效模型,能够列出实际问题中的反比例函数关系.
教学重点:理解反比例函数的概念..
教学难点:感受反比例函数是刻画世界数量关系的一种有效模型.
教学过程:
9.1反比例函数
教学目标:1、理解反比例函数的概念,会求比例系数.
1、已知y=y1+y2,y1与x成正比例,y2与x成反比例,并且当x=2时,y=-4,当x=-1时,y=5,求y与x的函数关系式.
2 举例说一说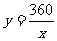 可以表示的实际意义.
可以表示的实际意义.
小结:本节课你有何收获?
作业:P64 练习 1 ,2 P64 习题 1,3
2、如果反比例函数的图象经过(1,-2),那么这个反比例函数的解析式为 .
3若函数
 是反比例函数,那么正比例函数
是反比例函数,那么正比例函数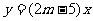 的图象经过第几象限?
的图象经过第几象限?
创新拓展:
1、某住宅小区要种植一个面积为1000 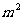 的矩形草坪,草坪长为 y m,宽为 x m,则 y关于 x 的关系式为____;它是反比例函数吗?
的矩形草坪,草坪长为 y m,宽为 x m,则 y关于 x 的关系式为____;它是反比例函数吗?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com