
3、要求出反比例函数的解析式,只要求出k即可.
例1 下列函数关系中,哪些是反比例函数?如果是,比例系数是多少?
(1)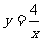 ;(2)
;(2)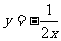 ;(3)
;(3)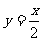 ;(4)
;(4)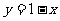 (5)
(5)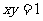
例2 将下列各题中y与x的函数关系与出来.
(1)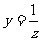 ,z与x成正比例;答:
,z与x成正比例;答:
(2)y与z成反比例,z与3x成反比例;答:
(3)y与2z成反比例,z与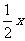 成正比例;答:
成正比例;答:
例3(1)y是x的反比例函数,当x=2时,y=3,求y与x之间的函数关系式。
(2)已知y1与x成正比,且y2与x成反比,且y=y1+y2,当x=1时,y=3,当x=2时y=3,求y与x之间的函数关系式。
例4当m为何值时,函数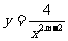 是反比例函数,并求出其函数解析式.
是反比例函数,并求出其函数解析式.
分析 由反比例函数的定义易求出m的值.
2、反比例函数的解析式又可以写成: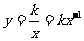 ( k是常数,k≠0).
( k是常数,k≠0).
上面两个问题中的函数具有怎样的共同特征?能否用一个统一的函数关系式把它们表示出来?说说你的看法。
归纳小结
上面两个函数中,两个变量的积为一个常数,都可以写成y=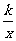 (k不等于零)的形式。
(k不等于零)的形式。
一般的,形如y=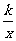 (k不等于零)的函数叫反比例函数
(k不等于零)的函数叫反比例函数
1、请同学们把正比例函数和反比例函数进行比较,说说它们有哪些不同?
(1)从形式上看,正比例函数y=kx是关于自变量的整式,反比例函数y=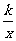 是关于自变量的分式;
是关于自变量的分式;
(2)从内涵上看,正比例函数y=kx的两个变量的商是非零常数,即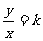 ,k是常数,且k≠0;反比例函数y=
,k是常数,且k≠0;反比例函数y=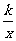 的两个变量积是一个非零常数;即xy=k,k是常数,且k≠0.
的两个变量积是一个非零常数;即xy=k,k是常数,且k≠0.
(3)从自变量和函数值取值范围来看,正比例函数y=kx中的自变量和函数值都可以为零,反比例函数y=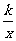 中的自变量和函数值都不能为零。
中的自变量和函数值都不能为零。
问题1 汽车从南京出发开往上海(全程约300km),全程所用时间t(h)随速度v(km/h)的变化而变化。
(1)你能用含有v的代数式表示t吗?
(2)利用(1)的关系式完成下表
|
v(km/h) |
60 |
80 |
90 |
100 |
120 |
|
t(h) |
|
|
|
|
|
随着速度的变化,全程所用的时间发生什么变化?
(3)速度是时间t的函数吗?为什么?
问题2、学校课外生物小组的同学准备自已动手,用旧围栏建一个面积为24平方米的矩形饲养场,假设它的一边长为x(米),求另一边的长y(米)与x的函数关系式。
答:
回顾小学所学的反比例,请举出两个反比例关系的事例。
(1):
(2):
见作业纸
P78,1、2
补1.已知y与2x-1成反比例,且当x=1时,y=2,那么当x=0时,y=________.
2. 若函数y=(m-1)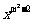 是反比例函数,则m的值等于( )
是反比例函数,则m的值等于( )
A.±1 B.1 C.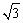 D.-1
D.-1
例1下列关系式中的y是x的反比例函数吗?如果是,比例系数k是多少?
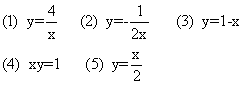
例2、已知变量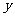 与
与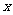 成反比例,当
成反比例,当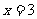 时,
时,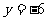 .
.
求(1)y与x之间的函数关系式;(2)当 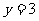 时,
时,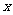 的值
的值
例3、已知y-2与x成反比例,且当x=2时,y=4,求y与x之间的函数关系式.
3、反比例函数的概念
一般地,如果两个变量x, y之间的关系可以表示成 y=(k为常数,k≠0)的形式,那么称y是x的反比例函数。k是比例系数。
反比例函数的自变量x 不能为零。
2、上面的函数关系式具有什么共同的特征?你还能举出类似的实例吗?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com