
3. 探索和经验总结,抽签的方法是合理的
教学过程:
日常生活中,我们有时会用抽签的方法来决定某件事情。
学生举例:
现实生活中,我们有哪些事可以用抽签的方法来解决。
创设情境:
问题一:有一张电影票,小明和小丽用抽签的方法来决定谁可以去看电影,于是准备了两张相同的小纸条,一张上面是“去”,另一张上面是“不去”,谁抽到“去”,则这个人就去看电影,这种方法公平吗?
同学们很快可以给出结果:公平
问题二:我们用抽签的方法从3名同学中选一名去参加某音乐会。事先准备三张相同的小纸条,并在1张纸条画上记号,其余2张纸条不画。把3张纸条放在一个盒子中搅匀,然后让3名同学去摸纸条,这种方法公平吗?
学生讨论:


提出质疑:
抽签有先有后,如果先抽的人抽到了,后抽的人就抽不到了。可是,如果先抽的人没有抽到,后抽的人抽到的机会就大了?
先抽的人与后抽的人中签的概率一样吗?
有老师引导学生探索:
下面我们就来算一算各人中签的概率:
假设这3名同学分别记作甲、乙、丙,他们抽签的顺序依次为:甲第一,乙第二,丙第三。三张小纸条中,画有记号的纸条记作A,余下的两张没有记号的纸条分别记作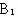 和
和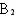 。
。
我们用表格列出所有可能出现的结果:
|
|
第一次 (甲抽) |
第二次 (乙抽) |
第三次 (丙抽) |
所有可能出现的结果 |
|
开始 |
A |
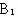 |
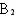 |
A 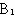 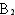 |
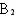 |
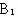 |
A 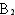 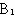 |
||
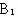 |
A |
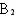 |
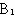 A A
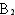 |
|
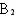 |
A |
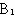 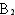 A A |
||
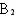 |
A |
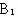 |
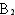 A
A 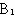 |
|
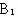 |
A |
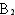
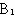 A A |
从上图可以看出,甲、乙、丙依次抽签,一共六种可能的结果,并且它们是等可能的。
A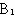
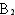 和A
和A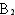
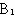 这两种结果为甲中签,P(甲中签)=1/3
这两种结果为甲中签,P(甲中签)=1/3
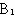 A
A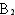 和
和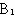
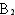 A这两种结果为乙中签,P(乙中签)=1/3
A这两种结果为乙中签,P(乙中签)=1/3
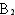 A
A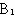 和
和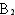
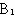 A这两种结果为丙中签,P(丙中签)=1/3
A这两种结果为丙中签,P(丙中签)=1/3
教师总结:
通过上面的分析我们看到,抽签虽然有先有后,但是先抽的人和后抽的人中签的可能性是一样的,因此对每个人来说都是公平的,所以不必挣着先抽签。
抽签的方法是合理的
课堂练习:
2. 通过探索,由学生总结“先抽的人与后抽的人”中签的概率是否一样
1. 让学生经历抽签的探索过程,感受抽签方法
9.1 抽签方法合理吗
教学目标:
义务教育阶段的数学课程,其基本出发点是促进学生全面、持续、和谐地发展,从而获得终身学习能力.本节课力求让学生感受到数学是解决实际问题和进行交流的重要工具,体会数学对促进社会进步和发展人类理性精神的作用,从而激发学生学习热情,增强学好数学的自信心,在独立思考的基础上,积极参与对数学问题的讨论,敢于发表自己的观点,从交流中获益,通过思考、归纳、总结、反思,从而学会学习.
充分“用教材”,以课本例题、习题为原型,设计具有典型性、开放性的题目,做到源于教材,又不脱离教材,从而活用教材.通过对抽签是否合理的猜想、探究、建模、验证,到设计公平合理的游戏规则,层层推进,进一步提高学生有条理的思考和表达的能力,培养学生发现问题和解决问题的能力.
学生学习活动的情况是现代数学课堂教学评价的一项重要指标.本节课从多层面开展课堂活动,既有民主和谐的师生互动式活动,更有学生的独立思考、演练、小组讨论、合作交流等学习活动.
“生活即数学,生活即教材”,从生活情景引入,从生活场景中提炼数学问题,建立数学模型,这样使学生找到了新知识的停靠点,参与的切入点和思维的激活点,促使学生应用已有知识去探索新知识,激发学生的学习动机和兴趣.
(二)迁移延伸
活动二:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com