
1. 理解不等式的性质,用不等式解简单的应用题.
9.1.2不等式的性质⑵ 学案
学习目标
3.
若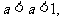 则
则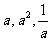 三者的大小关系是( )
三者的大小关系是( )
A. B.
B.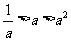 C.
C. D.
D.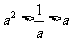
拓展延伸
⑴①如果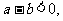 那么
那么
②如果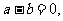 那么
那么
③如果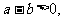 那么
那么
⑵由⑴,你能归纳出比较a与b大小的方法吗?请用语言叙述出来.
⑶用⑴的方法,你能否比较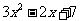 与
与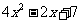 的大小?如果能,请写出比较过程.
的大小?如果能,请写出比较过程.
2. 无论x取什么数时,下列不等式总能成立的是( )
A.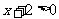 B.
B.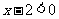 C.
C.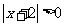 D.
D.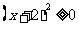
1. 用不等式表示:
⑴a与5的和是正数; ⑵b与15的差小于27; ⑶c的4倍大于或等于8;
⑷d与5的积不小于0. ⑸x的2倍与1的和是非正数.
3. 直接想出不等式的解集,并用数轴表示:
⑴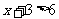 ; ⑵
; ⑵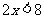 ; ⑶
; ⑶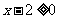 .
.
活动3课堂作业
2. 用不等式表示:
⑴a是正数; ⑵a 是负数;⑶a与5的和小于7;⑷a与2的差大于-1;⑸a的4倍大于8;⑹a的一半小于3.
1.
判断下列数中哪些是不等式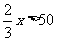 的解:76,73,79,80,74.9,75.1,90,60.你还能找出这个不等式的其他解吗?这个不等式有多少个解?
的解:76,73,79,80,74.9,75.1,90,60.你还能找出这个不等式的其他解吗?这个不等式有多少个解?
5. 一元一次不等式
什么叫做一元一次不等式?
点评:
⑴不等式分两大类:①表示大小关系的不等式,其符号类型有:“>”、“<”、“ ”、“
”、“ ”.
”.
“ ”读作“小于或等于”也可以说是“不大于”;“
”读作“小于或等于”也可以说是“不大于”;“ ”读作“大于或等于”也可以说“不小于”.②表示不等关系的不等式,其符号为“
”读作“大于或等于”也可以说“不小于”.②表示不等关系的不等式,其符号为“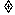 ”,读作“不等于”,它说明两个量之间的关系是不等的,但不明确谁大,谁小.③有些不等式不含未知数,有些不等式含未知数.
”,读作“不等于”,它说明两个量之间的关系是不等的,但不明确谁大,谁小.③有些不等式不含未知数,有些不等式含未知数.
⑵不等式的解集的表示方法:①用最简的不等式表示:如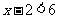 的解集为
的解集为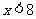 .②用数轴表示:如
.②用数轴表示:如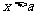 在表示 a的点上用空心圆圈表示不包括这一点,
在表示 a的点上用空心圆圈表示不包括这一点,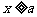 在表示a的点上用实心点表示包括这一点.
在表示a的点上用实心点表示包括这一点.
⑶一元一次不等式与一元一次方程的“两边”1.都是整式.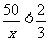 中x在分母位置,这个不等式不是一元一次不等式.
中x在分母位置,这个不等式不是一元一次不等式.
活动2 练习巩固
4. 解不等式的含义
什么叫解不等式?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com