
2、你认为作反比例函数图象时应注意哪些问题?
列表时,自变量的值可以选取绝对值相等而符号相反的一对一对的数值,这样既可简化计算,又便于描点。
1、作反比例函数y=的图象:
列表:
|
X |
-8 |
-4 |
-3 |
-2 |
-1 |
- |
|
1 |
2 |
4 |
8 |
|
y= |
|
|
|
|
|
|
|
|
|
|
|
描点:以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点。
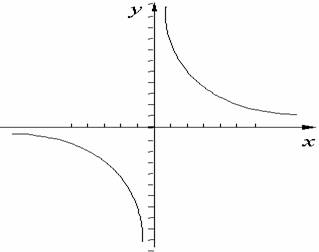 连线:用光滑的曲线顺次连结各点,即可得到函数y=的图象。
连线:用光滑的曲线顺次连结各点,即可得到函数y=的图象。
2、一次函数y=kx+b有什么性质?
答:一次函数y=kx+1的图象是一条直线。
当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小。
1、函数有哪几种表示方法?
答:图象法、解析法、列表法
3.例题教学
课本安排例1,是为了引导学生认识到:由于在反比例函数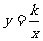 中,只要常数k的值确定,反比例函数就确定了.因此要确定一个反比例函数,只需要一对对应值或图象上一个点的坐标即可.
中,只要常数k的值确定,反比例函数就确定了.因此要确定一个反比例函数,只需要一对对应值或图象上一个点的坐标即可.
[教学过程设计建议(第三课时)]
例题教学
课本例2主要是引导学生会根据反比例函数的图象的某些特征,分析反比例函数的图象和性质.教学时,可以引导学生从以下两个方面进行探索:
(1)引导学生根据条件确定函数的类型,明确函数图象所在象限及有关性质;
(2)引导学生根据已知3点的横坐标,确定3点所在的象限,从而在它们各自所在的象限内比较大小.
2.探索活动
(1)先探索图象的特征;
(2)再用函数的观点分析反比例函数的特征.
1.情境创设
展示学生作业中6个反比例函数图象,引导学生进行分类并说明分类的依据.
2.探索活动
探索活动1 反比例函数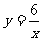 的图象.
的图象.
由于反比例函数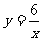 的图象是曲线型的,且分成两支.对此,学生第一次接触有一定的难度,因此需要分几个层次来探求:
的图象是曲线型的,且分成两支.对此,学生第一次接触有一定的难度,因此需要分几个层次来探求:
(1)可以先估计--例如:位置(图象所在象限、图象与坐标轴的交点等)、趋势(上升、下降等);
(2)方法与步骤--利用描点作图;
列表:取自变量x的哪些值?
描点:依据什么(数据、方法)找点?
连线:怎样连线?
(3)由于课本所给出的“描点”的点数较少,学生可能从这些点中还不能够充分感受“曲线”的形状,为此可以再多描一些点.,或利用计算机展示“点”的“加密”的过程,从而让学生对反比例函数的图象的认识逐渐清晰.
探索活动2 反比例函数 的图象.
的图象.
可以引导学生采用多种方式进行自主探索活动:
(1)可以用画反比例函数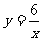 的图象的方式与步骤进行自主探索其图象;
的图象的方式与步骤进行自主探索其图象;
(2)可以通过探索函数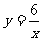 与
与 之间的关系,画出
之间的关系,画出 的图象.
的图象.
探索活动3 反比例函数 与
与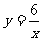 的图象有什么共同特征?
的图象有什么共同特征?
引导学生从通过与一次函数的图象的对比感受反比例函数图象“曲线”及“两支”的特征.
[教学过程(第二课时)]
1.情境创设
可以从复习一次函数的图象开始:你还记得一次函数的图象吗?在回忆与交流中,进一步认识函数图象的直观有助于理解函数的性质.转而导人关注新的函数--反比例函数的图象研究:反比例函数的图象又会是什么样子呢?
4.能根据图象分析并掌握反比例函数的性质,进一步感受数形结合的思想方法.
[教学过程(第一课时)]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com