9．2实际问题与一元一次不等式(一)

教学目标：

1．7

4620

①分别写出这两家运输单位运送这批水果所要收取的总费用y₁(元)和y₂(元)(用含s的式子表示)；

　②为减少费用，你认为果品公司应该选择哪一家运输单位运送水果更为合算？

设计思想

　本课主要采用“教师创设问题情境──学生自主探索与小组合作交流──师生共同概括明晰”的教学思路，把探索知识的主动权完全交给学生，让学生真正成为学习的主人。通过问题情境的设置，诱发学生的学习兴趣，营造师生之间民主和谐的学习氛围和每个学生平等参与学习的机会，从而达到培养学生善于思考、勤于学习的习惯和分析问题、解决问题的能力的目的。

　在教学中，要给予学生充分的思维空间，让学生亲身经历将实际问题抽象成数学模型并进行解释与应用的过程，使学生在对数学问题理解的同时，在思维能力、情感态度、价值观念等方面得到进一步发展，使自主探索、动手实践和合作交流成为学生学习的主要方式。要努力创设现实的、有意义的、富有挑战性的情境来说明学习数学知识的有用性、必要性，使学生认识到现实生活中蕴涵着大量的数学信息，启迪学生面对实际问题时，应主动尝试从数学角度运用所学知识和方法加以解决。

3.　　　 甲乙两家商店出售同样的茶壶和茶杯，茶壶每只定价都是20元，茶杯每只定价都是5元.两家商店的优惠办法不同：甲商店是购买1只茶壶赠送1只茶杯；乙商店是按售价的92%收款.某顾客需购买4只茶壶、若干只(超过4只)茶杯.去哪家商店购买更合算？

2.　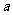　　 取什么数时，式子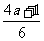表示下列数：

⑴正数；　　　　　⑵小于－2的数；　　　⑶0.

1.　　　 解下列一元一次不等式，并把它们的解集在数轴上表示出来：

⑴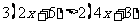　　　　⑵

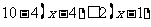
3.　　　 解一元一次不等式的一般步骤是什么？你认为有什么需要注意的？

活动2　探索用一元一次不等式描述实际问题中的不等关系

　问题　甲、乙两商店以同样的价格出售同样的商品，并且又各自推出不同的优惠方案：在甲商店累计购买100元商品后，再购买的商品按原价的90%收费；在乙商店累计购买50元商品后，再购买的商品按原价的95%收费.顾客怎样选择商店购物能获得更大优惠？

　⑴甲商店累计购_______元后可以优惠；乙商店累计购买_______元商品后可以优惠.

　⑵现在有4个人，准备分别消费40元、80元、140元、160元，那么去哪家商店更合算？为什么？

　⑶如果累计购买超过100元，那么在甲商店购物花费小吗？

　⑷累计购买超过100元而不到150元时，在哪个店购物花费小？累计购买恰好是150元时，在哪个店购物药费小？

　⑸根据甲乙商店销售方案，顾客怎样选择商店购物能获得更大优惠？你能为消费者设计一套方案吗？

活动3课堂小结

你对本节内容有哪些认识？

活动4　课堂作业

2.　　　 类比一元一次方程的解法，你能解下列一元一次不等式吗？试试看.

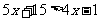⑴　　　　⑵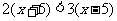

1.　　　 复习　解一元一次方程

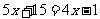⑴　　　　⑵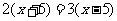

2.　　　 体会不等式是解决问题的有效数学模型.进一步强化用数学的意识.

重点

由实际问题中的不等关系列出不等式

活动1运用类比方法　探索一元一次不等式的解法

1.　　　 会解一元一次不等式. 会用不等式表示实际问题中的不等关系.