冬天到了,天气渐渐变冷,同学们在上学的路上未免会感觉到寒意,尤其是骑自行车上学的同学更觉得冷,妈妈们为了他们的孩子能过得舒服一些,都会给他们的孩子准备好帽子、手套来御寒.就拿手套来说吧,贵的可达几十元钱一双,便宜的呢,只要一、二元就可买到,但其质量和保暖程度肯定不相同,便宜的可能用的时间不长,而贵的对小孩来说不善于保护,又未免太奢侈了,作为家长肯定希望所买的东西价廉又物美,假设妈妈的要求是手套的价格不能超过6元,而小孩又不喜欢太便宜的,他们对家长的要求是所买的手套价格不能少于4元,同学们,如果你是商店售货员,你会拿什么价格的手套给他们选择呢?如果商店里的手套从每双2.5元至16元的各种价格都有,且每双不同的手套之间都是按逐渐提高0.5元的价格进行呈列的,你能确定他们的选择有几种吗?

　　 当然可以,太简单了,要使买的手套让家长和小孩都满意可让他们从每双4元至6元的这些物品中选,由于这档手套有4元/双,4.5元/双,5元/双,5.5元/双,6元/双共五种,故售货员只需从这五种价格的手套中取出供他们挑选,就能让母子同时满意.这里我们所用到的数学知识就是:如何确定不等式组的公共解集.今天我们就共同来探讨不等式组吧.

　　 通过培养学生的动手能力发展学生的感性认识与理性认识,培养学生独立思考的习惯.

　　 教材解读

　　 本节内容是在学习了不等式的解集之后的知识内容,在此基础上提出若某数同时满足几个不等式时,如何去确定这个数的取值范围,这就是不等式组的公共解集的确定,在实际生活中同样会遇到一个数所能满足的条件不止一个的问题,这就要用到不等式去确定其解.

　　 学情分析

　　 不等式的解集已经在前一节中学习并运用其解决实际问题,若由多个不等式构成的不等式组的解集如何确定呢?不等式的解集可类比方程的解进行求解,是否不等式组的解与方程组的解也类似呢?因此学生就会进行类比,进而可得出其解集的公共部分.

第1课时

　　 通过由一元一次不等式,一元一次不等式的解集、解不等式的概念来类推学习一元一次不等式组,一元一次不等式组的解集,解不等式组这些概念,发展学生的类比推理能力.

2.通过确定不等式组的解集与确定方程组的解集进行比较,抽象出这二者中的异同,由此理解不等式组的公共解集.

1.通过由学生动手操作:用各种不同长度的木棒去拼三角形,归纳出能拼出三角形的各边长之间的关系和不能拼成三角形的三边的特征,目的是归纳出同时符合几不同条件的不等式的公共范围,即不等式组的解集.毛

　弟弟上午八点钟出发步行去郊游，速度为每小时4千米；上午十点钟哥哥从同一地点骑自行车去追弟弟.如果哥哥要在上午十点四十分之前追上弟弟，问哥哥的速度至少是多少？

　已知5x-2y＝6，当x满足6≤7x-1＜13时，请确定y的取值范围．

　A．-1　　 B．0　C．1　　 D．4

　A．5　　 B．4　C．3　　 D．无数个

　A．a＝3　 b＝5　　　　　　　　　　　　　 B．a＝-3　 b＝-5

　C．a＝-3　 b＝5　　　　　　　　　　　　 D．a＝3　 b＝-5

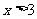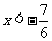23、　24、　25、　26、3≤x＜5　27、至少胜6场　28、6个孩子，26个水果。

1、公共部分　2、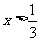，　3、无解　4、　5、0,1　6、1＜x＜11　7、元　8、≥　9、2＜x＜5　10、10　11---20、BCDCC　CAADB　21、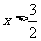　22、